Задача 1. За какое время тело, нагретое до 100о, охладится до 25о в комнате с температурой 20о, если до 60о оно охладилось за 20 мин. (По закону Ньютона скорость охлаждения тела в воздухе пропорциональна разности температуры воздуха).
Решение. Пусть в момент времени t после начала охлаждения тела его температура будет То, тогда, с одной стороны, скорость изменения температуры тела выразится формулой 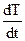 . С другой стороны, по закону Ньютона скорость охлаждения тела пропорциональна разности температур тела и воздуха в комнате. т.е. она равна
. С другой стороны, по закону Ньютона скорость охлаждения тела пропорциональна разности температур тела и воздуха в комнате. т.е. она равна 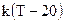 , здесь k - коэффициент пропорциональности, зависящий от массы, теплопроводности, формы тела.
, здесь k - коэффициент пропорциональности, зависящий от массы, теплопроводности, формы тела.
Сравнивая оба полученных выражения для скорости изменения температуры, получим:
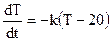
(знак минус, т.к. как температура тела уменьшается). Получили ДУ первого порядка с разделяющимися переменными. Решая его, получим общее решение:
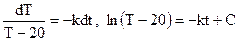 . (*)
. (*)
Произвольную постоянную С и коэффициент k можно найти из начальных условий. Подставляя в (*) t=0 мин., Т=100о, получим 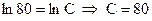 .
.
При t=20 мин., Т=60о, следовательно:
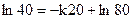
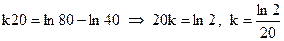 .
.
Таким образом, частное решение ДУ, удовлетворяющее всем условиям задачи, будет 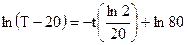 или
или 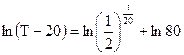 ,
, 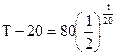 .
.
Теперь выясним, через сколько времени температура тела станет раной 25о. Подставляя вместо Т число 25, находим t:
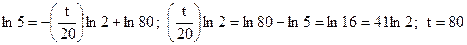 .
.
Следовательно, тело остынет до температуры 25о через 80 мин.
Задача 2. Найти: 1) семейство кривых, для которых угловой коэффициент касательной равен ординате точки касания; 2) кривую этого семейства, проходящую через точку
Р(2, 5).
Решение. ДУ искомого семейства у/=у или 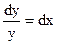 . Проинтегрировав обе части равенства, получим
. Проинтегрировав обе части равенства, получим 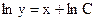 или
или 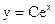 . Определим значение С, соответствующее начальным значениям:
. Определим значение С, соответствующее начальным значениям:
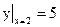 ;
; 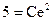 ;
; 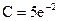 .
.
Следовательно, 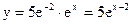 - искомая кривая (проходящая через точку Р).
- искомая кривая (проходящая через точку Р).
Пример 3. Найти кривые, проходящие через точку N(0, 1), для которых площадь треугольника, образованного касательной, ординатой точки касания и осью абсцисс, есть величина постоянная, равная 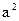 .
.
Решение. Пусть точка М с координатами (х, у) принадлежит искомой кривой (рис. 1). Тогда МА – отрезок касательной к кривой, причем 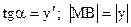 .
.
|


 У
У

 М(х, у)
М(х, у)

0 А В х
Рис. 1.
Это дифференциальное уравнение с разделяющимися переменными. Решая его, получим:
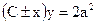 .
.
Учитывая, что кривые проходят через точку N(0, 1), найдем величину С:
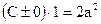 ,
, 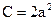 .
.
Следовательно, уравнения искомых кривых имеет вид
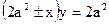 .
.
 2015-05-13
2015-05-13 3572
3572

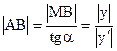 . По условию
. По условию 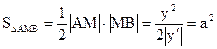 . Отсюда
. Отсюда 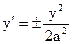 .
. 







