Ступенчатой функции

Для многих часто применяемых функций (например, дельта-функция, единичная ступенчатая функция, cosω₀t, sinω₀t и др.) преобразования Фурье, к сожалению, не существуют в обычном смысле. Тем не менее удобно обобщить технику лреобразований Фурье и на эти функции.

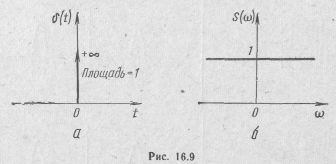
Учитывая выражения (14.12), с помощью формулы (16.3) на­ходим спектральную плотность дельта-функции (рис. 16.9, а)

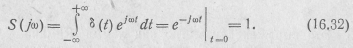
Таким образом, δ(t)-функции соответствует равномерно рас­пределенная спектральная плотность, спектр такой функции имеет бесконечно большую ширину (рис. 16.9,6).

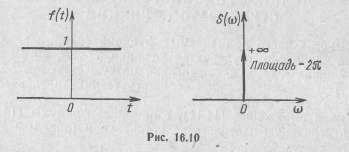
Заметим теперь, что на основании свойства частотно-временной двойственности или дуальности преобразований Фурье, если спект­ром δ(t)-функции является S(jω) =S(ω) = 1, то спектром функции S(t)=l будет 2πδ(ω) (рис. 16.10). Действительно, обратное преоб­разование Фурье от единицы (S(jω) = l) может быть записано как

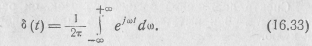
Взаимной заменой переменных t и ω получаем

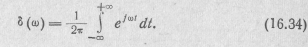
Заменив в этом выражении ω на -ω и учитывая, что δ(ω) = - δ(—ω), так как δ(ω)—четная функция, находим

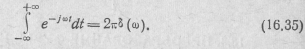
Это выражение известно как лемма Римана — Лебега. Хотя оно получено не совсем формализованно, существует его строгое доказательство.

Таким образом, спектральная функция постоянной величины, равной единице, есть δ-функция с площадью, равной 2π, взятая в частотной области (см. рис. 16.10).

Спектральная плотность любой постоянной α будет в а раз больше:

F [а] = 2 π а δ(ω). (16.36)

Спектр постоянной бесконечно узок, он расположен в районе частоты ω=0 и имеет бесконечно малую ширину, стремящуюся к нулю,

Используя полученные соотношения, можно найти преобразования Фурье и спектральную плотность гармонических функций cos ω₀t и sinω ₀t. Для этого достаточно использовать свойство преобразований Фурье — умножение функции времени на косинус или синус (теоре м а о модуляции) (табл. 16.1), учитывая выражение (16.36);

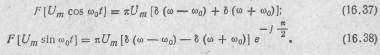
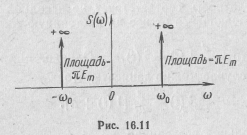
Спектр функций U_m cos ω₀t и U_m sinω ₀t, так же как и постоянной величины, бесконечно уз о к, его ширина бесконечно мала. Но в отличие от спектр а по­стоянной о нс о сред о т о ченв районе частот ω=ω₀ и ω= -ω₀ (рис. 16.11). Нали-

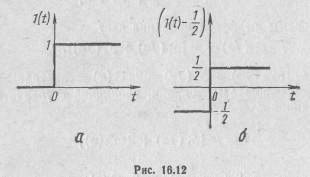
чие здесь двух частот: положительной и отрицательной — объясняется особен­ностью представления синусоидальных колебаний на плоскости комплексных величин.

Единичная ступенчатая функция (рис. 16..12,а) не является абсолютно интегрируемой (ее площадь не имеет конечного значе­ния). Поэтому попытка непосредственного применения преобразо­вания Фурье для нахождения спектральной плотности такой функ­ции приводит к расходящемуся интегралу, который, строго говоря (если пользоваться обычными определениями и правилами мате­матики), вычислить нельзя.

Однако стремление распространить спектральный метод, ши­роко применяемый для решения многих технических и физических задач, на рассмотрение единичных скачков приводит к попыткам

обойти возникающую при этом трудность различными приемами, которые часто приводят к неверному результату. Например, пред­ставляя 1(t) как предел (при 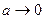) от экспоненциального им­пульса, получают

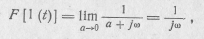
что не соответствует истине, так как найденная таким образом спектральная плотность соответствует не исходной функции l(t), а функции, отличающейся от нее на постоянную составляющую ¹ / ₂ (рис. 16.12,6).

Известно, что 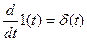. Однако, с другой стороны, вболее общем случае можно записать, что

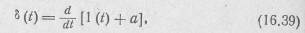
где а — произвольная постоянная.

Прямое преобразование Фурье от левой и правой части этого выражения

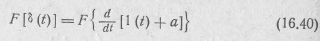
с учетом теоремы дифференцирования дает

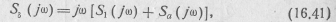
где S_δ(jω) = 1; S₁(jω) и S _a (jω) = 2πaδ( ω)— спектральная плот­ность соответственно δ(t) -функции, единичной ступенчатой функ­ции и постоянной а.

Отсюда

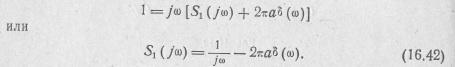
Найдем постоянную а в этом выражении. Обратное преобра­зование Фурье от его левой и правой части дает -

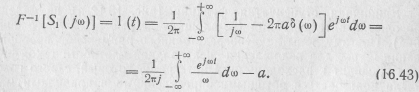
Здесь

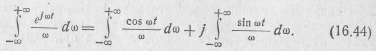
Кроме того, известно, что

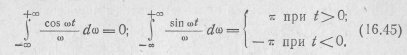
Учитывая это, а также то, что при t<0 l(t)=0, из выражения (16.43) получаем, 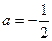, что после подстановки в формулу

(16.42) дает

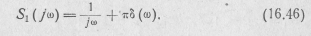
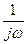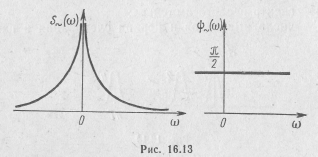
Здесь первое слагаемое есть спектральная плотность пе­ременной составляющей функции 1(t), а второе 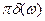—спектраль­ная плотность ее постоянной составляющей. Спектральные харак­теристики переменной составляющей

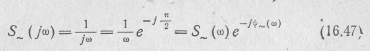
представлены на рис. 16.13.