Спектры пачек импульсов

К числу широко применяемых на практике сигналов относится пачка (серия) импульсов. Например, при обзоре радиолокатором цели от нее отражается и поступает на вход приемника последо­вательность из определенного числа импульсов, следующих через равные промежутки времени.

Допустим, что сигнал (пачка импульсов) состоит из конечного числа периодически повторяющихся импульсов произвольной формы. Пусть начало отсчета проходит через середину первого цмпульса (рис. 16.14). Найдем спектр сигнала,

На основании теоремы линейностии теоремы о сдвиге (табл. 16.1) спектральная плотность пачки импульсов

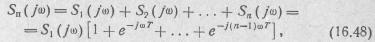
где S₁(jω) —спектр первого импульса;

п и Т — число импульсов и период следования в пачке.

В квадратных скобках получена геометрическая прогрессия, знаменатель которой 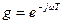.Сумма геометрической прогрессии, как известно, определяется дробью 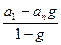, где а ₁и а_п — пер­вый и последний члены прогрессии. Следовательно,

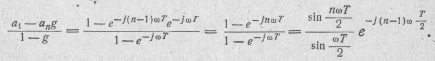
Таким образом,

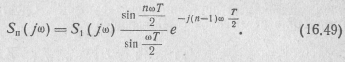
Модуль спектральной плотности пачки импульсов

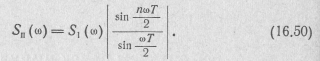
После нормирования по его значению S_П(0) при ω = 0 получаем модуль нормированной спектральной плотности

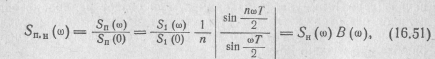
где 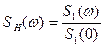-модуль нормированной спектральной плотности или нормированной АЧС импульса в пачке;

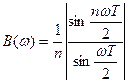- функция частоты, не зависящая от формы импульсов и определяемая лишь их числом и периодом следования,

Полученное выражение справедливо для пачек импульсов лю­бой формы. С его помощью, зная спектр импульса в пачке и вид функции B(ω), можно построить спектр всей пачки импульсов. Построение можно провести путем простого перемножения двух функци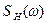й и .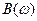

Рассмотрим подробнее функцию 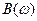. Легко заметить, что ее числитель и знаменатель одновременно обращаются в нуль при 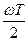, кратном π, т. е. 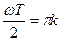, где k =0, 1,2,…. Раскрывая получающуюся при этом неопределенность по правилу Лопиталя, находим, что в этих случаях B(ω) = 1, так как

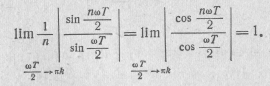
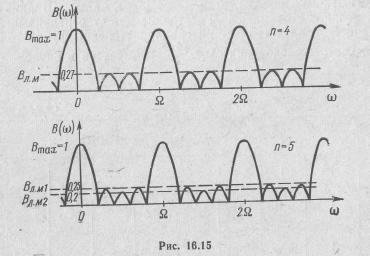
В интервале частот от 0 до 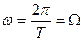числитель дроби в B (ω), а следовательно, и функция B(ω) принимают нулевое зна­чение п —1 раз. Периодичность числителя функции B(ω) в п раз выше, чем знаменателя. Графики функции B(ω) имеют лепестко­вую структуру (рис. 16.15). В общем случае график состоит из

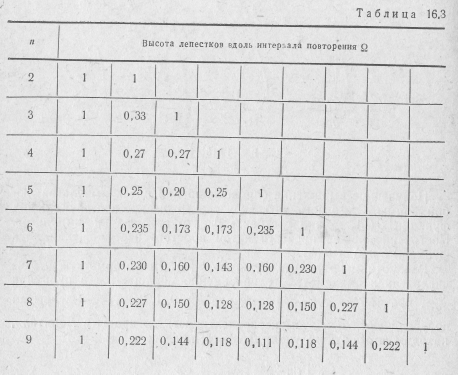
больших и малых лепестков. Высота больщих лепестков опре­деляется максимальным значением B_max = 1, а высоты малых ле­пестков—-локальными максимумами В_л._м функции B(ω). Число локальных максимумов и их значения можно найти путем иссле­дования функции B(ω) или с помощью специальных таблиц (табл. 16.3). Большие лепестки вдвое шире малых. Ширина всех малых лепестков одинакова. Расстояние между серединами боль­ших лепестков представляет интервал повторения функции B(ω), равный частоте следования 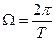импульсов в пачке.

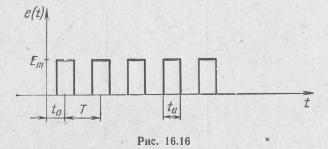
Рассмотрим в качестве примера спектр пачки прямоугольных видеоимпульсов. Пусть n=5 и 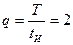(рис. 16.16). Для прямоугольного видеоимпульса в соответствии с выражением

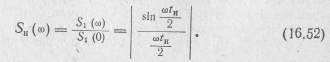
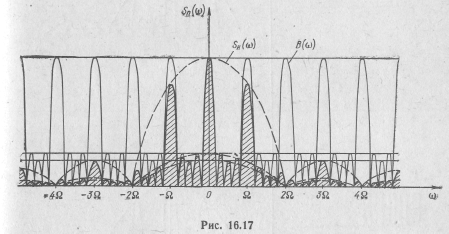
График этой функции определяется кривой 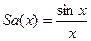(см. рис. 15.5) и пересекает ось частот в точках, соответствую­щих частотам qΩ = 2Ω, 4Ω,..., кратным скважности. Построение спектра пачки показано на рис. 16.17. На нем в общих координат-

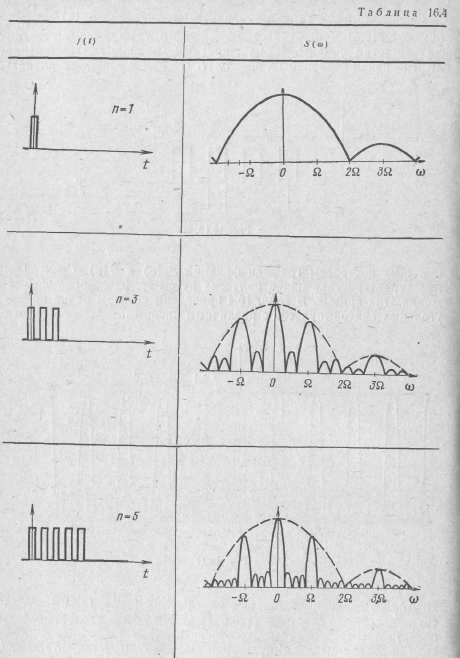
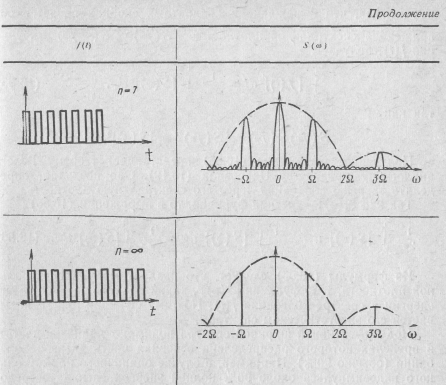
ных осях построены графики функций S_H(w) и B(ω). Спектраль­ная характеристика пачки получена путем графического перемно­жения этих кривых. В табл. 16.4 приведены спектры пачки прямо­угольных видеоимпульсов с различным числом п.

Анализ значений локальных максимумов (табл. 16.3) и ампли­тудно-частотных спектров (табл. 16.4) позволяет сделать выводы о связи спектров последовательности пачек и одиночных импуль­сов. С ростом числа импульсов п большие лепестки сужаются, высота малых лепестков уменьшается, а их число растет; спектр постепенно вырождается из сплошного в линейчатый и при 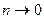превращается в дискретный.