Функций электрических цепей

Для установления характера операторных передаточных функ­ций линейных пассивных электрических цепей с сосредоточенными

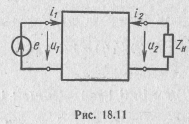
параметрами рассмотрим схему электрической цепи, приведенную на рис. 18.11.

Выбрав независимые контуры таким образом, чтобы ветвь с источником э,д. с. е входила только в первый контур, а ветвь

с током i₂ — только во второй контур, получим систему контурных уравнений в операторной форме:

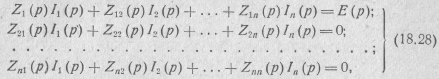
где

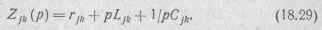
Из полученной системы уравнений найдем

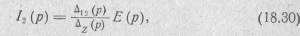
где Δ_z (р) —определитель системы контурных уравнений цепи (18.28);

Δ₁₂ (p) —его алгебраическое дополнение, полученное путем вычеркивания в Δ_z(р) первой строки и второго столбца и умножения на (—1)¹⁺².

Из выражения (18.30) получим

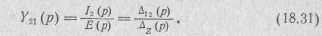
Из системы уравнений (18.28) можно получить и все остальные виды операторных передаточных функций электрической цепи.

Все эти функции, так же как Y ₂₁ (p), будут содержать отношение определителя системы Δ_z(p) и его алгебраических дополне­ний первого порядка Δ₁₁(p) и Δ₁₂(p), элементами которых яв­ляются простые рациональные функции (18.29).

При раскрытии определителя Δ_z(p) и его алгебраических до­полнений над их элементами производят толькй операции умно­жения, сложения и вычитания, в результате которых из рациональ­ных функций получаются также только рациональные функции.

Поэтому операторные передаточные и входные функции элек­трических цепей являются рациональными функциями оператора р с вещественными коэффициентами, т. е. представляют собой отно­шение двух полиномов W(p) и V(p), все коэффициенты которых вещественны:

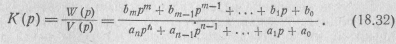
Представив полиномы числителя и знаменателя К(р) в виде произведения простых множителей, получим

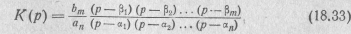
где β_k — корни числителя К(р);

а_k — корни знаменателя К(р).

При 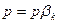передаточная функция становится равной нулю, а при р = а_k она становится равной, бесконечности. Поэтому 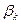на­зывают нулями передаточной функции, а а_k — ее полюсами. Сле­дует отметить, что если степень полинома числителя передаточной функции W (p) меньше степени полинома ее знаменателя V(p), то нули передаточной функции К(р) будут и при ρ= 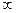. Причем кратность этих нулей будет равна разности степеней полиномов знаменателя и числителя передаточной функции К(р).

Нули и полюсы передаточной функции могут быть веществен­ными или попарно комплексно-сопряженными, поскольку их про­изведение должно дать вещественные коэффициенты bk и a_k по­линомов числителя и знаменателя К(р). Из выражений ( 18.25) и (18.32) следует, что

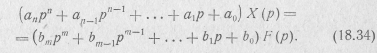
На основании теоремы о дифференцировании оригинала при нулевых начальных условиях, при которых и определена К(р), от уравнения для изображений (18.34) перейдем к дифферен­циальному уравнению для оригиналов

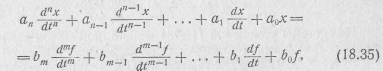
где x= x(t) — выходная величина (реакция цепи);

f=ƒ(t) —входная величина (воздействие на входе цепи). Из приведенных выражений видно, что если приравнять нулю знаменатель V(p) передаточной функции, то получим характери­стическое уравнение электрической цепи

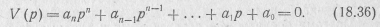
Это обстоятельство налагает дополнительные ограничения на вид полинома знаменателя передаточной функции электрической цепи, т. е. на вид полинома V(p), который обычно называют ха­рактеристическим полиномом электрической цепи.

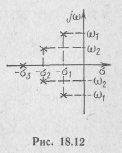
Так как свободные колебания в пассивных электрических це­пях носят затухающий характер, то нули характеристического полинома (полюсы передаточной функции) таких цепей должны иметь отрицательную вещественную часть, т. е. должны распола­гаться в левой полуплоскости (рис. 18.12). Такой полином назы­вают полиномом Гурвица.

В идеализированных пассивных цепях, составленных лишь из элементов L и С, свободные колебания не убывают по амплитуде, поскольку здесь первоначально запасенная энергия не расходуется на тепловые потери. Поэтому в цепях без потерь корни их харак-

теристйческих уравнений (полюсы передаточных функций) пред­ставляют собой пары мнимых сопряженных чисел ƒω_k и - ƒω_k, которым соответствуют незатухающие гармонические колебания. Однако чисто мнимые корни ƒω_k и -ƒω_k. должны быть про­стыми. Действительно, если бы такие корни имели каждый крат­ность m >1, то соответствующее им решение имело бы вид [9]

.

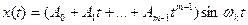При m >1 колебания в цепи с течением времени возрастали бы по амплитуде, чего в пассивной цепи быть не может.

Пассивных электрических цепей, в которых свободные колебания не убывают по ампли­туде, на практике также не существует.

Однако в электрических цепях с очень малыми потерями амплитуды свободных ко­лебаний убывают весьма медленно и приве­денная выше идеализация об отсутствии по­терь в цепи является очень полезной при ана­лизе электрических цепей и особенно при их синтезе.

Если известны нули и полюсы передаточ­ной функции цепи, то можно, составив выра­жение вида (18.33), найти саму функцию, за исключением постоян­ного вещественного множителя b_т/а_п, т. е. нули и полюсы переда­точной функции определяют эту функцию с точностью до постоян­ного вещественного множителя, играющего роль масштабного коэффициента.

По расположению нулей и полюсов передаточной функции можно судить о свойствах электрической цепи. Если все полюсы расположены только на отрицательной вещественной полуоси, то переходной процесс в цепи носит апериодический характер. Если имеются сопряженные полюсы в левой полуплоскости, то пере­ходный процесс носит характер затухающих колебаний. Причем чем ближе расположены полюсы к мнимой оси, тем медленнее за­тухают эти колебания, т. е. тем больше длительность переходного процесса.

По заданной передаточной функции можно создать цепь с за­данными свойствами, т. е. произвести синтез электрической цепи. Вследствие того что одной и той же передаточной функции могут соответствовать несколько различных схем, задача синтеза носит неоднозначный характер.

Таким образом, операторные передаточные функции линейных пассивных электрических цепей с сосредоточенными параметрами обладают следующими свойствами:

1.Они являются рациональными функциями оператора р с ве­щественными коэффициентами (18.32).

2.Пули и полюсы этих функций могут быть вещественными или попарно комплексно-сопряженными,

3.Полюсы этих функций могут располагаться только в левой полуплоскости, т. е. полиномы знаменателей этих функций яв­ляются полиномами Гурвица. Полюсы передаточных функций це­пей, состоящих из элементов L и С, располагаются на мнимой осп и являются простыми.

4.Нули этих функций могут располагаться как в левой, так и в правой полуплоскости. Дополнительные ограничения на распо­ложение нулей и полюсов налагаются как видом схемы цепи, так и видом входящих в нее элементов.