Полиномов электрических цепей

В предыдущем подразделе было показано, что характеристиче­ским полиномом пассивной электрической цепи является полином Гурвица, т. е. полином с вещественными коэффициентами, все нули которого расположены в левой полуплоскости р.

Полином Гурвица степени п

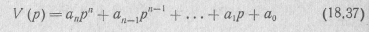
можно представить в виде произведения:

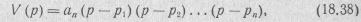
где р _k— нули полинома;

α _n — вещественное положительное число.

Все нули полинома р_k являются либо вещественными отри­цательными числами, либо попарно комплексно-сопряженными числами с отрицательной вещественной частью.

Вещественным отрицательным нулям р_k=-α_k<0 в разложе­нии (18.38) соответствуют линейные множители (p + ah) с веще­ственными положительными коэффициентами 1 и α_k.

Паре комплексных сопряженных нулей 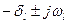соответствует произведение двух линейных множителей:

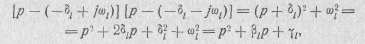
которое представляет собой полином второй степени с веществен­ными положительными коэффициентами 1, ß _l и γ _l.

Следовательно, полином Гурвица степени п может быть пред­ставлен в виде произведения полиномов первой и йторой степени с вещественными положительными коэффициентами:

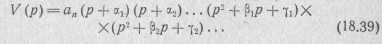
Отсюда следует, что полином Гурвица содержит все степени переменной р, от нулевой до n -й, и все его коэффициенты поло­жительны.

Поэтому, для того чтобы полином степени п был полиномом Гурвица, необходимо, чтобы полином содержал все степени пере­менной р oт нулевой до n -й и чтобы все его коэффициенты были вещественными положительными числами. Это условие является не­обходимым. Однако для полиномов третьей и более высоких степеней оно не является достаточным.

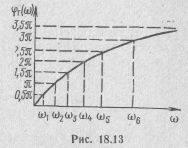Исследуем свойства полиномов Гурвица при p=jω, т. е. комплекса полинома Гурвица V(jw). Подста­вив p=jω в формулу (18.39), по­лучим

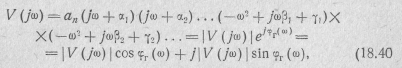
где |V jω)| —модуль комплекса полинома Гурвица;

φ_г(ω) —его аргумент, равный сумме аргументов отдельных

множителей. Аргумент линейного множителя (ƒω + a_k) равен

а аргумент квадратичного множителя (-ω² + jωß _l +γ _l) равен

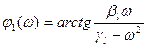. (18.42)

Из выражений (18.41) и (18.42) видно, что с изменением ча­стоты ω от 0 до со аргумент каждого из линейных множителей (18.40), монотонно возрастая, получает приращение на угол π /2, а каждого из квадратичных множителей — на угол π. Поэтому с изменением частоты ω от 0 до 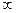аргумент 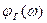комплекса по­линома Гурвица степени п, монотонно возрастая, получает прира­щение на угол n π/2.

Для примера на рис. 18.13 приведен график аргумента ком­плекса полинома Гурвица седьмой степени.

Таким образом, для того чтобы полином степени п был поли­номом Гурвица, необходимо, чтобы аргумент комплекса этого полинома при изменении частоты ω от 0 до 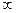получал прираще­ние на угол n π/2. Это условие является и достаточным.

Рассмотрим поведение вещественной и мнимой частей ком­плекса полинома Гурвица. Подставив p=jω в формулу (18.37), ролучим

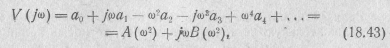
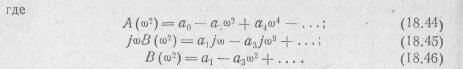
Из этих выражений видно, что вещественная часть комплекса полинома Гурвица содержит лишь четные, а мнимая часть — лишь нечетные степени частоты ω.

Из выражений (18.40) и (18.43) следует, что

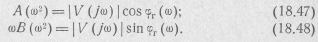
Отсюда видно, что вещественная часть комплекса полинома Гурвипа обращается в нуль всякий раз, когда его аргумент равен нечетному числу π/2, т. е. когда φ_г(ω)=±(2k+ 1)π/2, а мнимая часть — когда его аргумент равен целому числу π, т. е. когда φ_г(ω)= ±kπ.

Так как аргумент комплекса φ_г(ω) монотонно возрастает от нуля при ω = 0 до nπ/2 при ω= 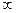, то с ростом ω от 0 до ею после­довательно обращается в нуль то мнимая, то вещественная части полинома V(jω).

Отсюда следует, что все нули вещественной и мнимой частей комплекса полинома Гурвица на оси jω являются простыми и че­редуются между собой, т. е. между любыми двумя смежными нулями полинома A(ω²) расположен один нуль полинома ωВ(ω²), и наоборот.

Поэтому степени полиномов А(ω²) и ωВ(ω²) всегда отличаются на единицу. Это же следует и из того, что ни один из коэффициен­тов полинома Гурвица не может быть равен нулю.

Из рассмотренного следует, ·po вещественную и мнимую части комплекса полинома Гурвица можно представить в виде произве­дений вещественных множителей:

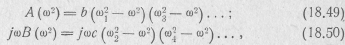
где 0<ω₁<ω₂<ω₃<ω₄….;

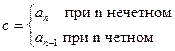
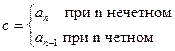
Если в последних выражениях перейти от jω к оператору р, тодля полинома Гурвица получим выражение

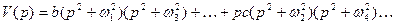(18.51)

Если четную или нечетную часть этого полинома умножить на положительную пострянную величину, то новый полином будет

также полиномом Гурвица, так как чередуемость нулей вещест­венной и мнимой частей комплекса этого полинома в этом случае не нарушается.

Если же нечетную часть этого полинома умножить на —1, то новый полином V(— р) будет называться полиномом, сопряженным с полиномом Гурвица. Все его нули будут располагаться в пра­вой полуплоскости р.

Рассмотренные свойства полиномов Гурвица могут быть ис­пользованы при обосновании некоторых критериев устойчивости и методов синтеза электрических цепей.