Пусть отрезок [ a,b ] разбит точками на n частичных отрезков 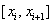 . Сплайном степени m называется функция
. Сплайном степени m называется функция 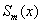 , обладающая следующими свойствами:
, обладающая следующими свойствами:
1) функция 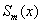 непрерывна на отрезке [ a,b ] вместе со своими производными до некоторого порядка p;
непрерывна на отрезке [ a,b ] вместе со своими производными до некоторого порядка p;
2) на каждом частичном отрезке 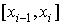 функция совпадает с некоторым алгебраическим многочленом
функция совпадает с некоторым алгебраическим многочленом 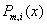 степени m.
степени m.
Разность m-p между степенью сплайна и наивысшим порядком непрерывной на отрезке [ a,b ] производной называют дефектом сплайна. Кусочно-линейная функция является сплайном первой степени с дефектом, равным единице. Действительно, на отрезке [ a,b ] сама функция 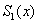 (нулевая производная) непрерывна. В то же время на каждом частичном отрезке
(нулевая производная) непрерывна. В то же время на каждом частичном отрезке 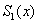 совпадает с некоторым многочленом первой степени.
совпадает с некоторым многочленом первой степени.
ПРИМЕР 3. Построение параболического сплайна.
Пусть дан фрагмент таблицы значений функции:
| x | -1 | ||
| y | 1.5 | 0.5 | 2.5 |
Требуется построить параболический сплайн дефекта 1.
Так как строится сплайн 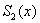 , то он будет представлен двумя полиномами 2-ой степени:
, то он будет представлен двумя полиномами 2-ой степени:
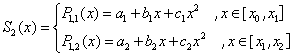 .
.
Функция 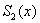 должна удовлетворять условиям:
должна удовлетворять условиям:
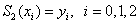 - это есть условие интерполяции;
- это есть условие интерполяции;
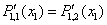 - это есть условие непрерывности первой производной.
- это есть условие непрерывности первой производной.
Таким образом, получили 5 условий для нахождения 6-сти неизвестных. Два условия дополнительно накладывают на сплайн в граничных точках.
Возьмем, например дополнительное граничное условие следующего вида 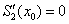 .
.
Тогда получим систему уравнений относительно неизвестных коэффициентов 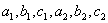 :
:
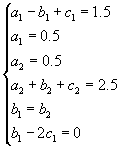
Эта система легко решается:
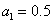 ,
, 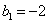 ,
, 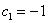 ,
, 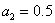 ,
, 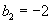 ,
, 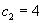 .
.
Таким образом:
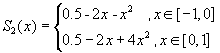 .
.
Наиболее широкое распространение получили сплайны 3 степени (кубические сплайны) 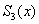 с дефектом равным 1 или 2. Система для осуществления сплайн-интерполяции кубическими полиномами предусматривает несколько встроенных функций. Одна из них рассмотрена в примере.
с дефектом равным 1 или 2. Система для осуществления сплайн-интерполяции кубическими полиномами предусматривает несколько встроенных функций. Одна из них рассмотрена в примере.
ПРИМЕР 4. Построение сплайн-интерполяции (рис. 10.4).
% Построить интерполяцию сплайнами функции Рунге
% Введём функцию Рунге
f = inline('1./(1+25*x.^2)');
% Вычислим таблицу значений
x = linspace(-1, 1, 10);
y = f(x);
% Вычислим сплайн-интерполяцию
xx = linspace(-1, 1, 100);
yy = spline(x, y, xx);
% Начертим графики
axes('NextPlot', 'Add');
plot(x, y, 'LineWidth', 2);
% Красным на графике - аппроксимация, жирным - исходная функция.
plot(xx, yy, 'Color', 'r');
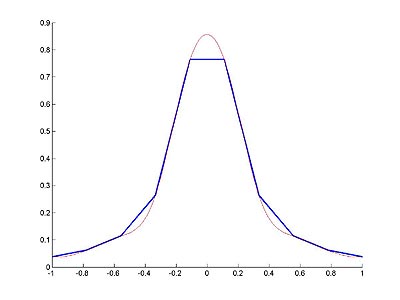
Рис. 10.4 - построение сплайн-интерполяции
Погрешность приближения кубическими сплайнами.
Пусть функция f имеет на отрезке [ a,b ] непрерывную производную четвертого порядка и 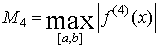 .
.
Тогда для интерполяционного кубического сплайна справедлива оценка погрешности: 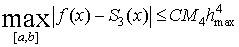 .
.
 2015-05-13
2015-05-13 3920
3920
