Сложение взаимноперпендикулярных колебаний

В результате сложения взаимноперпендикулярных колебаний получаются сложные в общем случае по виду траектории движения. Поэтому мы рассмотрим частный случай, когда складываемые колебания имеют одинаковые частоты, но разные амплитуды и фазы. В этом случае отдельные составляющие можно записать в виде 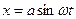и 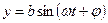. Здесь 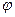- сдвиг фаз между складываемыми колебаниями.

Для определения вида траектории результирующего движения из закона движения следует исключить время. Для этого из первого выражения значение гармонической функции подставим во второе. Тогда получим, что:

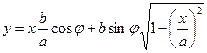
Для удобства последующего анализа выражение лучше представить в форме:

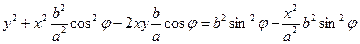
Даже в этом простом случае уравнение траектории для произвольного сдвига фаз между отдельными колебаниями принимает сложный вид. Мы рассмотрим частные случаи сдвига фаз.

а) 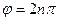. При таком сдвиге фаз уравнение траектории принимает вид

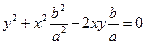
Упрощая выражение, получаем, что 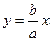т.е. траектория представляет собой прямую линию, которая лежит в первом и третьем квадрантах.

б) 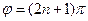. При таком сдвиге фаз уравнение траектории преобразуется к виду

.

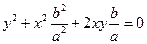Отсюда следует, что 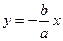, т.е. и в этом случае траектория представляет собой прямую линию с тем же наклоном, но она лежит уже во втором и четвёртом квадрантах.

в) . Уравнение траектории для такого сдвига фаз имеет вид

,

Рис. 108

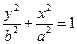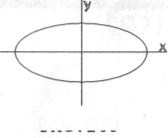т.е. представляет собой эллипс. Следует заметить, что как при сдвиге фаз 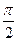, так и при 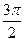уравнение траектории имеет один и тот же вид. Но характер движения точки вдоль своей траектории будет различным. В начальный момент времени 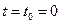смещение вдоль оси X равно нулю, а вдоль оси Y +b и - b соответственно. При дальнейшем движении точки по траектории смещение вдоль X увеличивается и принимает положительные значения, т.е. точка движется по траектории вправо. Это означает, что при сдвиге фаз 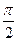точка должна двигаться по направлению хода часовых стрелок, а при 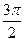против хода. Таким образом, такое изменение фазы приводит к изменению направления движения вдоль траектории. Рассмотренный случай сложения взаимноперпендикулярных колебаний приведен на рис.108.

Траектории результирующего движения при сложении взаимноперпендикулярных колебаний одинаковой частоты представляют собой только частный случай так называемых фигур Лиссажу. Фигурами Лиссажу называют траектории, описываемые точкой, совершающей одновременно два гармонических колебания во взаимноперпендикулярных направлениях. Вид таких траекторий зависит от соотношения между частотами складываемых колебаний, между их фазами и амплитудами. Если частоты отдельных колебаний не совпадают, как в рассмотренном выше случае, то в общем случае разность фаз между колебаниями будет изменяться с течением времени, вследствие чего картина размывается, и фигуры Лиссажу не наблюдаются. Но если частоты складываемых колебаний относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в начальное положение, т.е. получаются устойчивые фигуры сложной формы. При этом число касаний фигурой Лиссажу сторон прямоугольника, в который она вписана, даёт отношение периодов складываемых колебаний (их частот).

Вид фигур Лиссажу позволяет определить соотношение между частотами колебаний и их фазами. Даже если колебания не являются гармоническими, характерные особенности фигуры Лиссажу сохраняются, искажается только её форма. Таким образом, по виду фигуры Лиссажу можно определить соотношение между частотами и фазами складываемых колебаний, а также оценивать, насколько сильно они отличаются от гармонических. На рис.109 приведены некоторые фигуры Лиссажу для различных соотношений между частотами складываемых колебаний и сдвига фаз между ними.

Рис. 109

16.16. Гармонический анализ периодических движений.

Из изложенного выше материала следует, что в результате сложения гармонических колебаний можно получить периодическое, но негармоническое колебание. В конце прошлого века Фурье доказал, что справедливо и противоположное утверждение: любое периодическое движение можно представить в виде суммы гармонических составляющих. Математически это представление называется рядом Фурье.

Согласно Фурье, любой периодический процесс 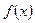, протекающий с частотой 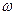может быть представлен бесконечным тригонометрическим рядом

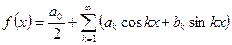(341)

или

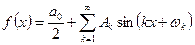(342)

При анализе периодических движений оба представления Фурье эквивалентны. Мы

будем пользоваться разложением Фурье в форме(341)

На амплитуды отдельных гармонических составляющих накладываются определённые ограничения, и они вычисляются по приведенным ниже соотношениям:

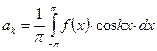(343)

и

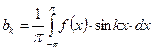(344)

где 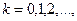а пределы интегрирования определяются тем промежутком, в котором определена сама изучаемая функция 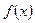. В приведенном случае функция определена в промежутке .

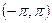Постоянная 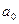разложения в ряд Фурье определяется из соотношения:

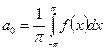(345)

При вычислении коэффициентов Фурье 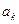и 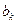часто бывает полезно пользоваться тем, что если функция 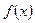четная в промежутке 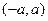, т.е. 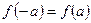, то

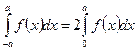(346)

а если функция 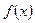нечётная, т.е. 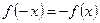, то

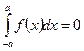(347)

Пользуясь этими общими правилами вычисления коэффициентов Фурье, рассмотрим разложение в тригонометрический ряд нескольких частных типов периодических колебаний, часто встречающихся в практике физических измерений и работе различных приборов.

а) Колебания прямоугольной формы. Колебания прямоугольной формы (рис. 110) могут быть представлены функцией

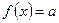, в промежутке 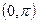и 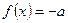в промежутке 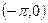, т.е. функция 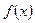в данном

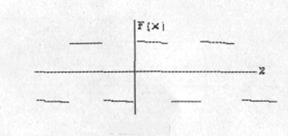случае является нечётной. Вне указанного промежутка функция повторяется с периодом 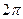, является периодической.

Рис.110

Так как исследуемая функция является нечётной, то в соответствии с (347) постоянный член разложения Фурье равен

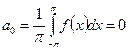(348)

Из соотношения (343)определяем коэффициенты Фурье :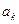

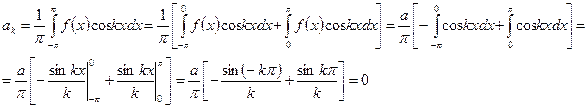(349)

Коэффициенты Фурье 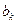определяются из (344):

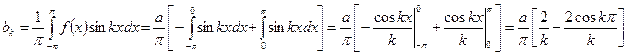
Как видно, коэффициенты 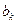принимают различные значения в зависимости от номера члена ряда (номера гармоники). Для нечётных гармоник (нечётных значений k)

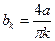(350)

а для четных

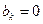(351)

Учитывая полученные значения коэффициентов разложения в ряд Фурье (348), (349), и (350), можно окончательно записать ряд Фурье для колебаний прямоугольной формы в виде

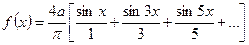(352)

Заметим, что разложение Фурье для этого случая состоит только из нечётных гармоник, амплитуды которых уменьшаются обратно пропорционально номеру гармоники.

б) Колебания пилообразной формы

Периодические колебания пилообразной формы, представленные на рис. 111, можно описать функцией 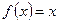, определяемой в промежутке 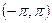. При других значениях аргумента 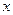функция повторяется с периодом .

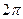Как видно, 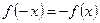, т.е. функция является нечётной, поэтому из (347) следует, что

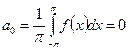(352).

Коэффициенты Фурье 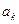определяется в соответствии с (343)

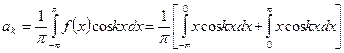(353).

Значение интеграла 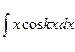удобно находить по правилу интегрирования по частям. По этому правилу, если подынтегральное выражение можно представить в виде 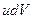, то с точностью до постоянной интегрирования можно записать:

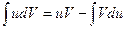(354).

Полагая 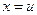и 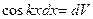, находим далее, что 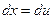, а 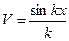. Используя правило (354) интегрирования по частям, можно записать, что (с точностью до постоянной интегрирования)

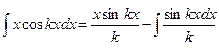(355).

Учитывая это, значения коэффициентов 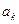в форме (353) перепишем в виде

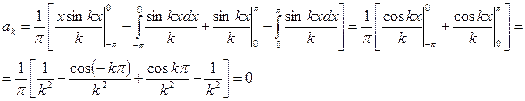(356).

Коэффициенты 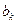определяются из (354):

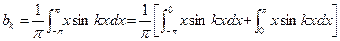(357).

Интегралы записанного вида также удобно находить по правилу интегрирования по частям. В этом случае полагаем 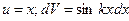. Учитывая это, получаем далее, что 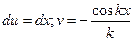. С учётом этих обозначений и используя правило (354), получаем:

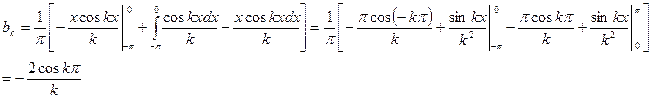
Таким образом, коэффициенты Фурье 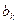при чётных значениях равны

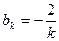(358)

а при нечётных

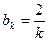(359)

С учётом найденных коэффициентов (352),(356),(358), и (359) разложение в тригонометрический ряд Фурье колебаний пилообразной формы записывается в виде

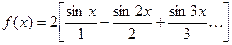(360)

в) Колебания треугольной формы

Колебания треугольной формы (рис.112) описываются функцией 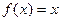, определённой в промежутке 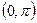и 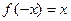, определённой в промежутке 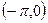. Так как 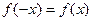, функция является чётной, а для чётной функции по (346)

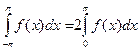(361)

Прежде всего определим по (345) значение постоянного члена разложения:

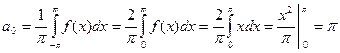(362)

Определяем далее по (343) коэффициенты :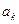

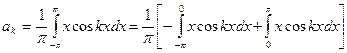
В этом выражении значения интегралов находим по правилу интегрирования по частям, как в предыдущем случае:

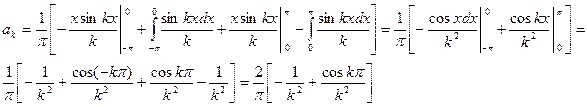
Для чётных значений

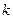
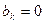(363)

а для нечётных

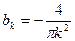
Используя найденные значения коэффициентов 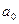, 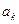и, записываем разложение Фурье для колебаний треугольной формы в виде

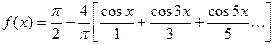(365)

16.17. Спектральный состав периодических колебаний.

В общем случае периодические колебания прямоугольной формы могут отличаться от вида, представленного на рис.110, где длительности самих импульсов и промежутков между ними одинаковы. На практике часто встречаются и периодические колебания прямоугольной формы, у которых длительность пауз между импульсами не равны длительности самих импульсов. Колебания такой формы представлены на рис.113.

Колебания такой формы характеризуются, прежде всего, скважностью. Скважностью называют безразмерный коэффициент, численно равный отношению периода повторения импульсов Т к их длительности:

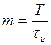(366)

Периодическую последовательность импульсов можно представить суммой гармонических составляющих в виде ряда Фурье. При анализе такого рода колебаний, особенно когда фазовые соотношения не играют роли, часто определяют только амплитуды гармоник или

Энергию колебаний (пропорциональную квадрату амплитуды), соответствующие каждой из гармоник. В этом случае постоянный коэффициент разложения Фурье не играет роли, и достаточно определить лишь коэффициенты 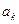и .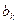

Если на графике зависимости амплитуды от частоты отложить вертикальные отрезки прямых, равные в выбранном масштабе амплитуде колебаний, при частотах, равных частотам гармоник, получим спектр изучаемого периодического процесса (рис.114):

В приведенном на рис.114 спектре колебаний присутствуют только нечетные гармоники, амплитуды которых уменьшаются с ростом номера гармоники.

В качестве примера рассмотрим расчет спектра периодических колебаний прямоугольной формы произвольной скважности по амплитудам гармоник и построение спектральных диаграмм для различной скважности.

Как было сказано выше, для построения спектральных характеристик достаточно лишь определить коэффициенты 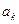и 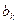разложение Фурье, определяющий амплитуды гармоник. Форма исследуемых колебаний представлена на рисунке 113. Из рисунка видно, что колебания описываются функцией 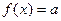, определяемой в промежутк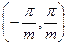е , где 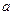- амплитуда колебаний, а 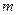скважность. Промежуток определяется фазой колебаний, соответствующий срезу импульса

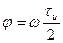
Выражая циклическую частоту через период колебаний и учитывая значение (346) скважности, получаем выражение фазы для среза импульса (значение границы промежутка, в котором определена функция ):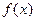

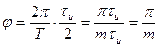
При таких границах промежутка коэффициент разложения Фурье по (343) равен

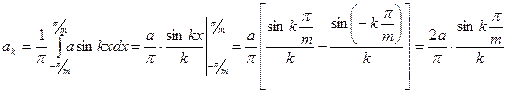(367)

Коэффициенты разложения 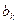определяем из (324):

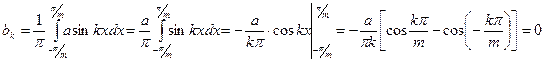(368)

Таким образом, исследуемые колебания могут быть представлены рядом Фурье

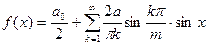(369)

Для определения спектрального состава колебаний как это следует из (369), достаточно определить амплитуды 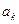соответствующих гармоник.

Отметим, что при увеличении пауз между импульсами появляются дополнительные члены разложения, дополнительные гармоники, при этом с увеличением пауз при сохранении длительности самого импульса период функции увеличивается, поэтому в разложении ее в ряд Фурье должны появляться составляющие со все меньшими частотами. Кроме того, следует учесть, что в разложении Фурье пропадают гармоники с частотами 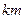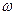, m – скважность, 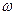- основная частота (основная гармоника), а k =1,2,3,…

Следовательно, при увеличении пауз между импульсами (увеличении скважности), будет уменьшаться основная частота и соответствующим образом изменяться спектр, в котором будет исключаться все меньшее числа гармоник. Спектр колебаний «уплотняется», основная частота с увеличением скважности приближается к нулю, а количество гармоник увеличивается. Постепенное увеличение скважности позволяет качественно оценить картину спектра для одиночного импульса. Очевидно, что при бесконечном увеличении скважности (в случае одиночного импульса) основная частота стремится к нулю, а спектр колебаний за счет появления все большего числа гармоник становится сплошным. Такой сплошной спектр уже нельзя описывать рядом Фурье, дискретным спектром. Одиночный импульс описывается интегралом Фурье

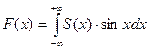(370)

Где величина S(x) называется функцией распределения и определяет закон распределения амплитуды колебаний по спектру (по частоте). В случае сплошного спектра нельзя говорить о составляющих колебания (импульса) определенной амплитуда, а можно только указывать среднее значение амплитуды в очень узком интервале частот, определяемое функцией распределения. Если же говорить об амплитуде (энергии) колебаний для конкретного значения частоты (т.е. для нулевого частотного интервала), то амплитуда колебания и, соответственно, энергия обращаются в нуль.

На практике (например, в радиолокации) используются не просто отдельные прямоугольные импульсы, а импульсы, заполненные незатухающими гармоническими колебаниями, период которых значительно меньше длительности импульсов. В этом случае абсолютный максимум амплитуды разложения соответствует основной частоте гармонического колебания, заполняющего импульсы, а дополнительных частот тем больше, чем меньше периодов гармонического колебания укладывается за время, равное длительности заполняемого импульса. При достаточно большом количестве периодов гармонических колебаний, укладывающихся за время импульса, практически можно учитывать только узкую область частот вблизи главного максимума, соответствующего основной частоте (частоте гармонических колебаний). Отсюда следует, что чисто гармонические колебания на практике отсутствуют. Колебания можно приближенно считать гармоническими в том случае, когда количество периодов этих колебаний за время одного импульса достаточно велико. Поэтому в спектре какого-либо гармонического колебания, длительность существования которого ограничена во времени, нельзя говорить о спектральной линии. Речь может идти о спектральной полосе, ширина которой зависит от соотношения между длительностью импульса и периодом гармонических колебаний, заполняющих импульс. Говоря о ширине спектральной линии (подразумевая спектральную полосу), имеют в виду обычно частотный интервал 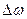, на границах которого функции распределения уменьшается до 0,7 своего максимального значения.

Степень монохроматичности колебаний можно оценивать выражением

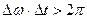
Из приведенного выражения следует, что большая монохроматичность излучения (меньший интервал 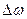) требует большего времени излучения (существования колебаний).

16.18. Нелинейные колебательные системы.

Линейными называются системы, свойства которых не изменяются при изменении их состояния, т.е. параметры системы, характеризующие ее свойства (например, масса, упругость, коэффициент трения для механических систем), не зависят от смещений и состояния, например, упругость пружины маятника с увеличением деформации перестает точно следовать закону Гука и т.д. Поэтому реальные механические системы можно рассматривать как линейные только приближенно, в определенных границах изменения ее параметров, когда ими можно пренебречь. Для большого числа систем эти пределы оказываются весьма широкими, поэтому широк и круг задач, в которых системы рассматриваются как линейные. В тех же случаях, когда изменениями параметров нельзя пренебрегать, сами системы уже следует рассматривать как нелинейные.

Линейные системы обладают рядом свойств, которые существенно упрощают их анализ. Процессы в линейных системах описываются линейными дифференциальными уравнениями (откуда произошло и само название систем). Вследствие этого, во-первых, линейные системы без искажения воспроизводят внешние воздействия, имеющие гармоническую форму, и, во-вторых, в линейных системах строго соблюдается принцип суперпозиции колебаний. Кроме того, линейные колебания изохронны, т.е. их частота не зависит от амплитуды колебаний.

В примерах колебаний рассмотренных в предыдущих параграфах (например, собственные колебания, вынужденные колебания и т.д.), возвращающая сила пропорциональна первой степени смещения, производных от смещения по времени различных порядков, называется линейным относительно самого смещения и его производных по времени. Если же в уравнении появляются более высокие степени смещения и его производных, то уравнение становится нелинейным. Например, при больших смещениях математического маятника от положения равновесия в разложении 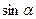уже нельзя пренебрегать более высокими степенями разложения по сравнению с первым членом.

Наиболее важным свойством линейных колебательных систем является то их свойство, что если система может одновременно принимать участие в двух движениях (в частности, колебательных), то результирующее смещение равно геометрической сумме принципа суперпозиции. В нелинейных же системах этот принцип не выполняется. Действительно, предположим, что нелинейная система описывается нелинейным дифференциальным уравнением.

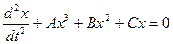
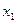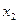Пусть записанное уравнение имеет два различных частных решения и , соответствующие различным начальным условиям. Для каждого из решений можно записать

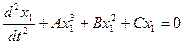
и

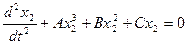
Если принцип суперпозиции будет соблюдаться, уравнению должно удовлетворять и решение 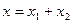. После подстановки 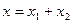в исходное уравнение получаем, что

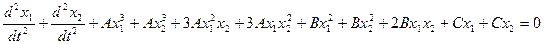
Как видно, из уравнения уравнение будет выполнятся только в том случае, если выполняются условия

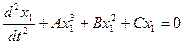
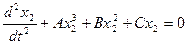
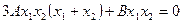
Первых два условия соблюдаются всегда, поскольку 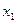и 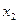являются решениями уравнения движения. Что касается последнего уравнения, то оно будет выполняться только в том случае, если коэффициенты 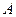и 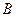равны нулю. Таким образом, принцип суперпозиции только для уравнений, у которого все коэффициенты при членах, содержащих во второй и более высоких степенях, равны нулю

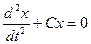
а это есть линейное дифференциальное уравнение.

Рассмотрим несколько примеров нелинейных механических колебательных систем. Сразу же отметим, для решения нелинейных дифференциальных уравнений не существует стандартных методов, в разных случаях для изучения нелинейных систем применяют специальные приёмы, которые позволяют получить лишь приближённое описание системы, приближённое решение уравнений, описывающих нелинейную систему. Поэтому для получения основных, характерных для всех нелинейных систем выводов воспользуемся частными примерами.

Нелинейной, например, называется является колебательная система с переменной упругостью. Переменная упругость (нелинейная зависимость упругости от деформации пружины) приводит к возникновению нелинейных колебаний, ещё раз отметим, что для нелинейных систем несправедлив принцип суперпозиции. Например, если поведение системы описывается дифференциальным уравнением движения 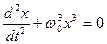и известны его частные решения, то подстановка их поочерёдно в исходное уравнение даёт следующий результат.

Как видно, движение каждого тела проходит по совершенно одинаковым законам с одной и той же частотой .

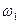б). В исходный момент времени 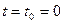оба тела отводятся от их положения равновесия на одинаковое расстояния в разные стороны и отпускаются без толчка. Начальное смещение и скорости тел в этом случае равны: 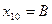, , 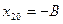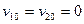. При таких начальных условиях, как это следует из (394), обращается в нуль амплитуда первой составляющей, т.е. оба тела будут совершать гармонические колебания с частотой 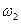. Амплитуда колебаний 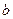определяются из (395), а начальная фаза колебаний- из (397):

.

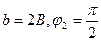Учитывая получены результаты, запишем законы движения тел и для этих начальных условий:

,

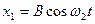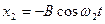
Получается, что и в этом случае движения каждого тела являются гармоническими, но колебания происходят в противофазе.

В). В исходный момент времени первое из тел отводится от положения равновесия на 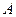, а второе- удерживается в его положении равновесия. Затем оба тела без толчка отпускают. Начальное смещения тел и их начальные скорости равны 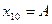, , 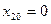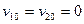. Учитывая это, из выражений (394),(395),(396),(397) находим значения амплитуд составляющих и начальные фазы колебаний: .

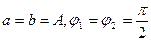C учётом полученных результатов можно в окончательном виде представить законы движения каждого из системы тел:

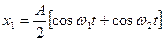
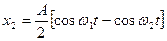
Таким образом, при рассмотренных начальных условиях,в отличие от описанных ранее, колебания тел не являются чисто гармоническими, а представляют собой сумму двух гармонических составляющих различных частот. В этом легко убедиться, если законы тел записать в виде:

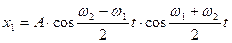
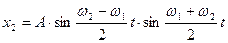
Для такого рода колебаний необходимо отметить весьма существенную деталь. Как видно из самих законов движения, амплитуды колебаний отдельных тел системы с течением времени периодически изменяются по гармоническому закону. При этом, если в некоторый момент времени амплитуда колебаний одного из тел системы обращается в нуль, то амплитуда второго тела в данный момент времени становится максимальной. Следовательно, в системе энергия колебаний каждого тела периодически изменяется. В те моменты времени, когда энергия колебаний одного из них равна нулю, энергия второго максимальна. Иначе говоря, с течением времени происходит передача энергии от одного из колеблющихся тел ко второму.