Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Ульяновский государственный технический университет
ОРТОГОНАЛЬНЫЕ И РОТОТАБЕЛЬНЫЕ ЦЕНТРАЛЬНЫЕ КОМПОЗИЦИОННЫЕ
ПЛАНЫ ЭКСПЕРИМЕНТА
Методические указания к выполнению лабораторных работ
по курсу «Математическое моделирование» для студентов направления 230401, квалификации 23040165
«Инженер-математик»
Составители: А. Г. Ташлинский
Г. Л. Минкина
Ульяновск 2005
УДК 681.3.01 (076)
ББК 32.96я7
И88
Ортогональные и рототабельные центральные композиционные планы эксперимента – методические указания к лабораторным работам по курсу «Математическое моделирование» / Сост.: А. Г. Ташлинский, Г. Л. Минкина. – Ульяновск: УлГТУ, 2005. – 40 с.
Методические указания разработаны в соответствии с программой курса «Математическое моделирование» и предназначены для студентов экономико-математического факультета направления 230401, квалификации 23040165 «Инженер-математик».
Указания посвящены построению и анализу эмпирических полиномиальных математических моделей второго порядка, удовлетворяющих критериям ортогональности и рототабельности. Рассмотрены вопросы получения оценок коэффициентов полинома по методу наименьших квадратов, проверки воспроизводимости опытов, исследованию статистической значимости оценок коэффициентов и проверки адекватности полученной математической модели.
Указания могут быть использованы при выполнении лабораторных работ по курсу "Математическое моделирование", а также при курсовом и дипломном проектировании.
Методические указания подготовлены на кафедре САПР.
Ил. 2. Табл. 10. Библиогр.: 6 назв.
Рецензент заведующий кафедрой прикладной математики и информатики УлГТУ, д-р физ.-мат. наук, профессор Валеев С. Г.
Одобрено секцией методических пособий
научно-методического совета университета
© А. Г. Ташлинский, Г. Л. Минкина, составление, 2005
© Оформление, УлГТУ, 2005
ОГЛАВЛЕНИЕ
1. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ.................................................................................... 4
2. ОРТОГОНАЛЬНЫЕ ЦЕНТРАЛЬНЫЕ КОМПОЗИЦИОННЫЕ ПЛАНЫ........................ 11
2.1. Составление матрицы планирования эксперимента............................................. 11
2.2. Порядок постановки опытов........................................................................................... 13
2.3. Проверка воспроизводимости опытов (однородности дисперсий).................... 13
2.4. Расчет оценок коэффициентов регрессионного уравнения................................. 14
2.5. Проверка адекватности полученной математической модели.................................
2.6. Переход к физическим переменным................................................................................
2.7. Пример выполнения ортогонального центрального композиционного
эксперимента..........................................................................................................................
2.8. Порядок выполнения работы......................................................................................... 21
2.9. Содержание отчета........................................................................................................... 21
Контрольные вопросы............................................................................................................. 21
3. РОТОТАБЕЛЬНЫЕ ЦЕНТРАЛЬНЫЕ КОМПОЗИЦИОННЫЕ ПЛАНЫ........................ 22
3.1. Составление матрицы планирования эксперимента............................................. 22
3.2. Порядок проведения эксперимента............................................................................. 22
3.3. Пример расчета рототабельного ЦКП......................................................................... 26
3.4. Порядок выполнения работы......................................................................................... 32
3.5. Содержание отчета........................................................................................................... 33
Контрольные вопросы............................................................................................................. 33
ПРИЛОЖЕНИЕ 1. TАБЛИЦА G-РАСПРЕДЕЛЕНИЯ........................................................... 34
ПРИЛОЖЕНИЕ 2. ТАБЛИЦА t-РАСПРЕДЕЛЕНИЯ............................................................. 35
ПРИЛОЖЕНИЕ 3. ТАБЛИЦА F-РАСПРЕДЕЛЕНИЯ........................................................... 36
ПРИЛОЖЕНИЕ 4. Работа с матрицами в mathcade.............................................. 37
БИБЛИОГРАФИЧЕСКИЙ СПИСОК......................................................................................... 39
ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
Построение математических моделей (ММ) реальных объектов невозможно без эксперимента, который является отправной точкой и критерием наших знаний и занимает главное место среди способов получения информации. Различают пассивный и активный эксперимент. Осуществление пассивного эксперимента не зависит от экспериментатора и ему приходится довольствоваться лишь ролью наблюдателя. Активный эксперимент, напротив, проводится в контролируемых и управляемых условиях. Однако все факторы, влияющие на исследуемый объект (или какой-то его параметр) предусмотреть, как правило, не удается. Кроме того, в сложных системах, зависящих от множества факторов, некоторые воздействия не могут контролироваться или управляться. Статистически воздействие таких факторов рассматривается как шум, наложенный на истинные результаты эксперимента. Для отделения интересующих экспериментатора факторов от шумового фона применяются специальные приемы.
Проведение активного эксперимента часто требует больших временных и материальных затрат, поэтому важно уметь получить необходимые сведения при минимальном числе опытов. Решить эту проблему призвана теория планирования эксперимента, представляющая собой раздел математической статистики и позволяющая ответить на вопросы:
– как спланировать эксперимент, обеспечивающий при требуемой точности результатов минимальные затраты времени и средств?
– как обработать результаты эксперимента, чтобы извлечь из них максимум информации для построения ММ объекта?
– какие выводы можно сделать по результатам эксперимента и какова достоверность этих выводов?
 При планировании эксперимента исследуемый объект представляется «черным ящиком» (рис. 1.1), на который воздействуют факторы
При планировании эксперимента исследуемый объект представляется «черным ящиком» (рис. 1.1), на который воздействуют факторы 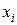 . Каждый фактор
. Каждый фактор 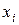 может принимать различные значения, которые называют уровнями фактора, а множество возможных уровней – областью определения фактора
может принимать различные значения, которые называют уровнями фактора, а множество возможных уровней – областью определения фактора 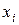 . Эта область может быть непрерывной и дискретной, ограниченной и неограниченной.
. Эта область может быть непрерывной и дискретной, ограниченной и неограниченной.
При выборе факторов необходимо учитывать требования к их совместимости и независимости. Совместимость предполагает допустимость любой комбинации факторов, а независимость – отсутствие между факторами корреляционной связи (это требование не всегда удается полностью выполнить, но сильная корреляционная связь недопустима).
К исследуемым параметрам (функциям отклика) также предъявляется ряд требований. Они должны быть:
– эффективными, то есть способствовать скорейшему достижению цели;
– универсальными (быть характерными не только для исследуемого объекта);
– статистически однородными, то есть определенному набору факторов 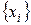 с точностью до погрешности эксперимента должно соответствовать определенное значение параметра
с точностью до погрешности эксперимента должно соответствовать определенное значение параметра 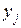 .
.
Кроме того, параметры должны выражаться количественно одним числом, иметь физический смысл и существовать при любом состоянии объекта.
Геометрическую интерпретацию параметра называют поверхностью отклика, а пространство, в котором строят эту поверхность, – факторным пространством. Размерность факторного пространства равна числу воздействующих факторов. Так, например, если их два, то это факторная плоскость.
При планировании эксперимента требуемых свойств ММ добиваются, выбирая условия проведения опытов. Множество точек факторного пространства, в которых проводится эксперимент, представляется с помощью плана эксперимента
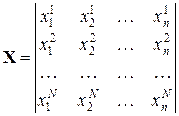 ,
,
где 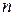 – число факторов;
– число факторов; 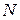 – число точек факторного пространства.
– число точек факторного пространства.
Точка
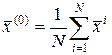
называется центром плана. Если центр плана совпадает с началом координат, то план называется центральным.
Если на исследуемый объект действует много факторов, механизм которых неизвестен, то для построения ММ объекта используют, как правило, алгебраические полиномы, называемые уравнениями регрессии. Полиномами можно описать любую аналитическую функцию как угодно точно. Однако с ростом степени полинома резко возрастает число оцениваемых параметров, поэтому обычно ограничиваются второй степенью. Например, для двух факторов 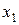 и
и 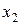 :
:
– полином 0-й степени 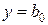 ;
;
– полином 1-й степени (линейная модель)
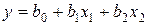 ; (1.1)
; (1.1)
– полином 2-й степени (квадратичная модель)
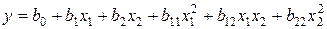 . (1.2)
. (1.2)
Обобщая можно записать
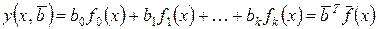 ,
,
где 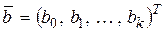 – вектор неизвестных параметров ММ, оценки которых
– вектор неизвестных параметров ММ, оценки которых 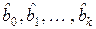 требуется найти путем обработки экспериментальных данных;
требуется найти путем обработки экспериментальных данных; 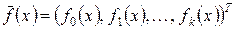 – вектор известных функций, выбранных для ММ, например, для (1.1) вектор
– вектор известных функций, выбранных для ММ, например, для (1.1) вектор 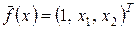 , для (1.2) –
, для (1.2) – 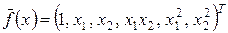 .
.
Пусть эксперимент проводится в 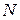 точках факторного пространства. Обозначим эти точки соответственно
точках факторного пространства. Обозначим эти точки соответственно 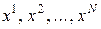 . Каждой
. Каждой 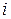 -й точке соответствует координата
-й точке соответствует координата 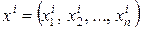 , где
, где 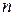 – число факторов. Результаты представлены вектором наблюдений
– число факторов. Результаты представлены вектором наблюдений 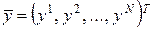 . Если в каждой точке
. Если в каждой точке 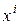 проведено
проведено 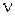 параллельных опытов и получены результаты
параллельных опытов и получены результаты 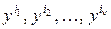 , то в качестве
, то в качестве 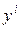 будем использовать среднее значение
будем использовать среднее значение
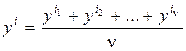 .
.
Оценки 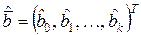 неизвестных коэффициентов ММ рассчитываются из уравнения
неизвестных коэффициентов ММ рассчитываются из уравнения 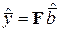 , где
, где
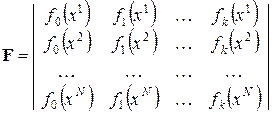 .
.
К оценкам 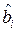 обычно предъявляются требования несмещенности (
обычно предъявляются требования несмещенности (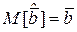 )и минимальности дисперсии (
)и минимальности дисперсии (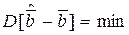 ). Возможны и другие критерии для понятия «наилучшая оценка», но приведенные выше два требования, приводящие при нормальном распределении результатов наблюдений к методу наименьших квадратов(МНК), позволяют провести статистический анализ полученных оценок и проверить адекватность ММ. Отметим также, что при МНК считается, что:
). Возможны и другие критерии для понятия «наилучшая оценка», но приведенные выше два требования, приводящие при нормальном распределении результатов наблюдений к методу наименьших квадратов(МНК), позволяют провести статистический анализ полученных оценок и проверить адекватность ММ. Отметим также, что при МНК считается, что:
– результаты эксперимента не содержат систематических погрешностей;
– результат в точке 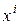 не зависит от результата в точке
не зависит от результата в точке 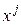 ;
;
– дисперсия результатов (дисперсия наблюдений) во всех точках эксперимента одинакова и равна 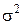 .
.
В случае невырожденности матрицы 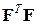 сумма
сумма
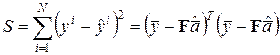
имеет единственный минимум (единственное решение) при
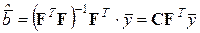 , (1.3)
, (1.3)
где матрица 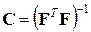 , имеющая размерность
, имеющая размерность 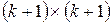 , называется дисперсионной матрицей, а матрица
, называется дисперсионной матрицей, а матрица 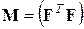 – информационной матрицей.
– информационной матрицей.
Оценки 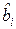 , рассчитанные в соответствии с (1.3), отличаются от истинных коэффициентов тем больше, чем больше погрешность наблюдений. Показателями точности оценок коэффициентов
, рассчитанные в соответствии с (1.3), отличаются от истинных коэффициентов тем больше, чем больше погрешность наблюдений. Показателями точности оценок коэффициентов 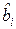 и зависимой переменной
и зависимой переменной 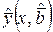 являются их дисперсии
являются их дисперсии 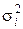 и
и 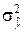 соответственно. Эти дисперсии зависят не только от дисперсии погрешности наблюдений
соответственно. Эти дисперсии зависят не только от дисперсии погрешности наблюдений 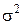 , но и от выбора структуры ММ и точек постановки опытов в факторном пространстве. При этом для ковариационной матрицы
, но и от выбора структуры ММ и точек постановки опытов в факторном пространстве. При этом для ковариационной матрицы 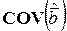 получаем
получаем
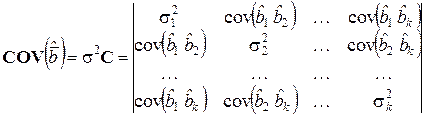 ,
,
где 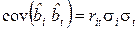 . Тогда дисперсия
. Тогда дисперсия 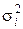 оценки
оценки 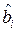 коэффициента
коэффициента 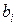
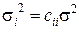 ,
,
а коэффициент корреляции между оценками 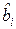 и
и 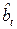
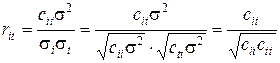 ,
,
где 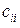 и
и 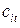 – соответствующие элементы дисперсионной матрицы
– соответствующие элементы дисперсионной матрицы 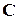 .
.
Рассмотрим пример. Пусть необходимо построить квадратичную ММ вида
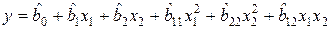 .
.
В этом случае матрица 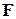 имеет вид:
имеет вид:
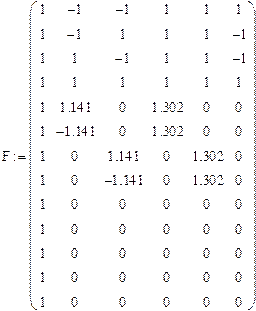
а матрица 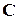 :
:
Условно это можно представить таблицей
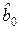
| 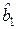
| 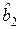
| 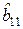
| 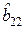
| 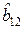
| |
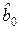
| 0,187 | – 0,109 | – 0,109 | |||
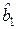
| 0,151 | |||||
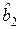
| 0,151 | |||||
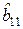
| – 0,109 | 0,254 | – 0,041 | |||
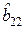
| – 0,109 | – 0,041 | 0,254 | |||
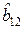
| 0,25 |
При этом коэффициент корреляции между оценками 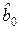 и
и 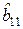 будет равен
будет равен
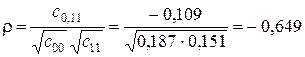 ,
,
между оценками 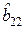 и
и 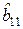
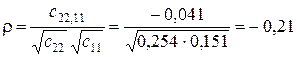 .
.
Таким образом, при известной дисперсии наблюдений 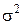 и предположении о нормальном законе распределения результатов наблюдений можно построить доверительный интервал
и предположении о нормальном законе распределения результатов наблюдений можно построить доверительный интервал
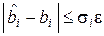
для заданной вероятности 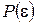 , где
, где 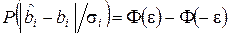 ;
; 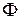 – функция Лапласа.
– функция Лапласа.
Дисперсию 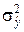 можно рассчитать по формуле
можно рассчитать по формуле
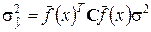 .
.
Если же дисперсия 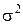 погрешности единичного наблюдения не известна, то ее можно оценить по экспериментальным данным, в частности, по остаточной сумме квадратов
погрешности единичного наблюдения не известна, то ее можно оценить по экспериментальным данным, в частности, по остаточной сумме квадратов 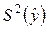 :
:
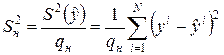 ,
,
где 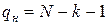 – число степеней свободы. Если в каждой точке факторного пространства проводится
– число степеней свободы. Если в каждой точке факторного пространства проводится 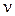 опытов, то оценку дисперсии погрешности единичного наблюдения корректнее находить с помощью соотношения
опытов, то оценку дисперсии погрешности единичного наблюдения корректнее находить с помощью соотношения
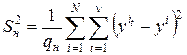 , (1.4)
, (1.4)
где 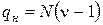 – число степеней свободы.
– число степеней свободы.
Если 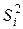 – оценка дисперсии
– оценка дисперсии 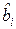 , то величина
, то величина 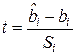 подчиняется
подчиняется 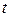 ‑распределению Стьюдента с числом степеней свободы
‑распределению Стьюдента с числом степеней свободы 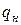 . Тогда для истинного значения
. Тогда для истинного значения 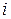 -го коэффициента с вероятностью
-го коэффициента с вероятностью 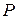 получаем доверительный интервал
получаем доверительный интервал 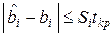 , где критическое значение
, где критическое значение 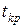 соответствует выбранной доверительной вероятности
соответствует выбранной доверительной вероятности 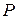 и числу степеней свободы
и числу степеней свободы 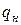 (прил. 2). Заметим, что в общем случае оценка
(прил. 2). Заметим, что в общем случае оценка 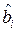 и ее дисперсия зависят от других коэффициентов. Поэтому если какой-то коэффициент исключается из ММ (например, в силу статистической незначимости), то оценки остальных коэффициентов и их дисперсии нужно пересчитать. При этом могут измениться как доверительные интервалы для
и ее дисперсия зависят от других коэффициентов. Поэтому если какой-то коэффициент исключается из ММ (например, в силу статистической незначимости), то оценки остальных коэффициентов и их дисперсии нужно пересчитать. При этом могут измениться как доверительные интервалы для 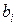 , так и выводы относительно их значимости.
, так и выводы относительно их значимости.
После расчета оценок коэффициентов необходимо проверить адекватность полученной ММ. Делают это, сравнивая погрешность ММ с величиной, характеризующей погрешность единичного наблюдения, которую оценивают сравнением результатов нескольких параллельных опытов (1.4). Дисперсию, характеризующую неадекватность ММ, можно оценить как
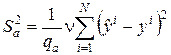 ,
,
где 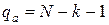 – число степеней свободы.
– число степеней свободы.
Гипотеза об адекватности ММ проверяется с помощью 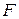 -критерия Фишера. Расчетное значение этого критерия представляет собой частное от деления оценки дисперсии неадекватности на оценку дисперсии единичного наблюдения
-критерия Фишера. Расчетное значение этого критерия представляет собой частное от деления оценки дисперсии неадекватности на оценку дисперсии единичного наблюдения
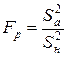 , (1.5)
, (1.5)
а критическое значение 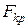 находят по соответствующим таблицам
находят по соответствующим таблицам
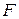 -распределения, используя числа степеней свободы числителя
-распределения, используя числа степеней свободы числителя 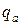 и знаменателя
и знаменателя 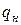 и требуемую доверительную вероятность
и требуемую доверительную вероятность 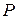 . Обычно выбирают
. Обычно выбирают 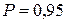 или
или 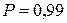 . Например, при
. Например, при 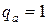 ,
, 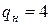 и
и 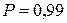 находим, что
находим, что 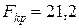
(прил. 3).
Заметим, что адекватность модели может быть проверена лишь в случае, когда число точек плана эксперимента больше числа оцениваемых параметров. Минимальному числу точек 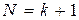 , которое уже не позволяет проверить адекватность модели, соответствует так называемый насыщенный план.
, которое уже не позволяет проверить адекватность модели, соответствует так называемый насыщенный план.
Условия проведения опытов могут свободно выбираться в пределах заданных границ. Выбор соответствующего плана эксперимента позволяет обеспечить ММ различные свойства. Наиболее распространенными являются следующие критерии.
Критерий ортогональности – когда получаемые оценки коэффициентов регрессионного уравнения не коррелированны. Применяется для упрощения вычислений, т. к. замена нулем любого коэффициента в ММ в этом случае не изменяет значений остальных коэффициентов. Обычно используется для отбора факторов, существенно влияющих на выходную величину.
Критерий рототабельности – когда дисперсия выходной переменной зависит от расстояния от центра плана и не зависит от направления (равная дисперсия на одинаковых расстояниях от центра плана). Этот критерий используется, если требуется обеспечить равную погрешность ММ на одинаковых расстояниях от центра плана.
Критерий A-оптимальности требует выбора такого плана, при котором матрица 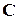 имеет минимальный след (минимальна сумма диагональных элементов).
имеет минимальный след (минимальна сумма диагональных элементов).
По смыслу это минимизация средней дисперсии оценок коэффициентов модели.
Критерий D-оптимальности требует минимизации определителя матрицы 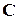 (минимизируется объем эллипсоида рассеяния погрешностей оценок коэффициентов модели).
(минимизируется объем эллипсоида рассеяния погрешностей оценок коэффициентов модели).
Критерий G-оптимальности требует достижения наименьшей величины максимальной дисперсии зависимой переменной.
Заметим, что критерии ортогональности и рототабельности обеспечивают ряд удобных и полезных свойств оценок коэффициентов, но никак не связаны с требованиями максимальной точности построения математической модели. Критерии A- и D-оптимальности требуют максимальной точности нахождения коэффициентов регрессии, в отличие от них G-критерий требует максимальной точности оценки зависимой переменной.
Все приведенные критерии предполагают, что вид модели известен. Если это не так, эксперимент вначале планируется, исходя из предположения о линейности модели относительно факторов. Проверяется адекватность полученной ММ, если линейная модель неадекватна – строят квадратичную. Для этого снова планируют эксперимент. Желательно, чтобы он включал точки плана для линейной модели, в которых эксперимент уже проведен. Если вид модели неизвестен, то, как правило, для исследователя более важна возможность проверки адекватности модели, чем точность оценки ее параметров.
В настоящих методических указаниях рассмотрена методика построения и свойства факторных планов для квадратичных моделей вида
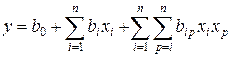 . (1.6)
. (1.6)
Заметим, что для возможности оценивания коэффициентов 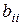 при
при 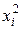 в уравнении (1.6) независимая переменная
в уравнении (1.6) независимая переменная 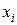 должна принимать, по крайней мере, три различных значения.
должна принимать, по крайней мере, три различных значения.
Факторный план для квадратичной модели может быть получен добавлением некоторого количества точек к «ядру» типа 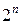 или
или 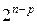 факторного плана линейной модели. Если добавить точку в центре плана и
факторного плана линейной модели. Если добавить точку в центре плана и 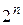 так называемых «звездных» точек с координатами
так называемых «звездных» точек с координатами 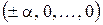 ,
, 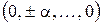 ,
, 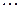 ,
, 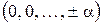 , то получим
, то получим
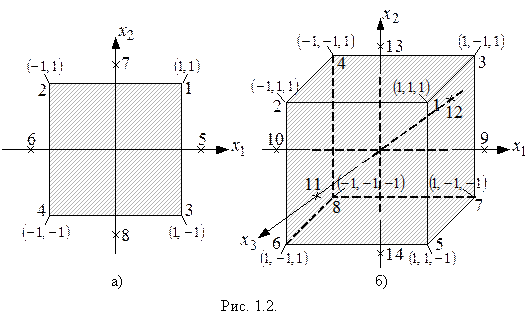
центральный композиционный план (ЦКП). Геометрическая интерпретация ЦКП при 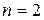 и
и 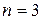 приведена на рис. 1.2 (а, б).
приведена на рис. 1.2 (а, б).
Выбором величины плеча 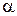 можно обеспечить различные свойства плана. Ниже рассмотрено построение ортогональных и рототабельных ЦКП.
можно обеспечить различные свойства плана. Ниже рассмотрено построение ортогональных и рототабельных ЦКП.
ОРТОГОНАЛЬНЫЕ ЦЕНТРАЛЬНЫЕ КОМПОЗИЦИОННЫЕ ПЛАНЫ
В ортогональных ЦКП плечо 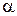 выбирают из условия обеспечения независимости (несмешанности) оценок коэффициентов регрессии. При этом одну точку берут в центре плана – тогда общее число точек плана
выбирают из условия обеспечения независимости (несмешанности) оценок коэффициентов регрессии. При этом одну точку берут в центре плана – тогда общее число точек плана 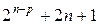 .
.
Для удобства расчетов и анализа результатов переходят к нормированному масштабу. Для этого масштабы факторов выбирают так, чтобы значение верхнего уровня в ядре плана соответствовало 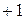 , а нижнего
, а нижнего 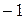 , тогда для
, тогда для 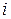 -го фактора
-го фактора
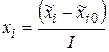 , (2.1)
, (2.1)
где 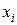 – нормированное значение;
– нормированное значение; 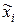 – натуральное значение;
– натуральное значение; 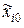 – основной уровень;
– основной уровень; 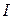 – интервал варьирования.
– интервал варьирования.
2.1. Составление матрицы планирования эксперимента
Для нахождения условий, обеспечивающих ортогональность, квадратичную модель (1.6) удобнее записать в виде
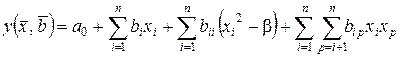 ,
,
где 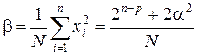 ;
; 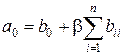 .
.
При этом матрица планирования (МП) эксперимента принимает вид, приведенный в виде табл. 2.1, где 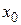 – фиктивная переменная, соответствующая коэффициенту
– фиктивная переменная, соответствующая коэффициенту 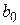 . В качестве ядра плана используется МП полного или дробного плана. Отметим, что не любые дробные планы, взятые в качестве «ядра», позволяют обеспечить ортогональность. Для получения некоррелированных оценок всех коэффициентов нужно, чтобы в матрице планирования не было одинаковых столбцов.
. В качестве ядра плана используется МП полного или дробного плана. Отметим, что не любые дробные планы, взятые в качестве «ядра», позволяют обеспечить ортогональность. Для получения некоррелированных оценок всех коэффициентов нужно, чтобы в матрице планирования не было одинаковых столбцов.
Из табл. 2.1 ясно, что одинаковые столбцы могут быть только у взаимодействий факторов. При этом на ортогональность столбцов взаимодействий выбор величины 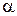 не влияет. Кроме того, парные взаимодействия должны быть несмешаны с линейными членами. При
не влияет. Кроме того, парные взаимодействия должны быть несмешаны с линейными членами. При 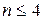 дробных планов, удовлетворяющих указанным требованиям, нет. При
дробных планов, удовлетворяющих указанным требованиям, нет. При 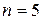 ,
, 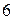 и
и 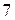 возможно использование планов типа
возможно использование планов типа 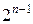 и только начиная с
и только начиная с 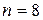 можно выбрать план
можно выбрать план 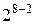 с генераторами, например,
с генераторами, например, 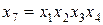 ,
, 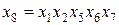 .
.
Рассмотрим, как выбрать плечо 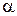 . Скалярные произведения любых двух столбцов, кроме столбцов при
. Скалярные произведения любых двух столбцов, кроме столбцов при 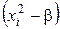 , равны нулю при любом
, равны нулю при любом 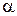 . Таким образом, достаточно найти
. Таким образом, достаточно найти 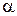 из условия, что скалярное произведение любых двух столбцов для
из условия, что скалярное произведение любых двух столбцов для 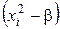 равно нулю.
равно нулю.
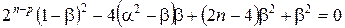 .
.
Таблица 2.1
Ортогональный ЦКП
| Номер точки | 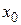
| 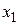
| … | 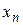
| 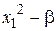
| … | 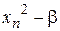
| 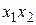
| … | 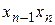
| |
| Ядро плана |
:
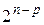
| +1 +1 +1 : +1 | +1 –1 +1 : –1 | … … … : … | +1 +1 +1 : –1 | 1 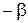 1
1 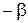 1
1 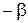 :
1
:
1 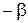
| … … … : … | 1 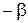 1
1 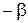 1
1 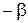 :
1
:
1 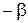
| +1 –1 –1 : +1 | … … … : … | +1 +1 +1 : +1 |
| Звез- дные точки | 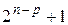
| +1 | 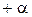
| … | 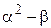
| … | 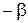
| … | |||
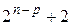
| +1 | 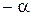
| … | 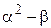
| … | 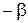
| … | ||||
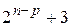
| +1 | … | 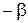
| … | 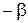
| … | |||||
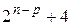
| +1 | … | 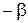
| … | 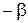
| … | |||||
| : | : | : | : | : | : | : | : | : | : | : | |
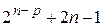
| +1 | … | 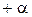
| 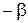
| … | 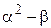
| … | ||||
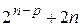
| +1 | … | 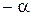
| 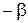
| … | 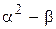
| … | ||||
| Центр плана | 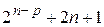
| +1 | … | 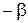
| … | 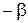
| … |
Откуда получаем
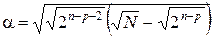 .
.
Значения 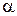 и
и 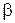 , обеспечивающие ортогональность плана при некоторых
, обеспечивающие ортогональность плана при некоторых 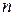 , приведены в табл. 2.2.
, приведены в табл. 2.2.
Таблица 2.2
Параметры ортогональных ЦКП
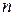
| Ядро плана | 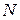
| 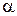
| 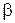
| Элементы матрицы 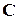
| |||
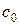
| 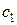
| 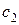
| 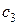
| |||||
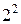
| 1,000 | 0,6667 | 0,1111 | 0,1667 | 0,5000 | 0,2500 | ||
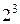
| 1,215 | 0,7300 | 0,6667 | 0,0913 | 0,2298 | 0,1250 | ||
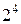
| 1,414 | 0,8000 | 0,0400 | 0,0500 | 0,1250 | 0,0625 | ||
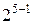
| 1,547 | 0,7700 | 0,0371 | 0,0481 | 0,0871 | 0,0625 | ||
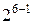
| 1,722 | 0,8430 | 0,0222 | 0,0264 | 0,0564 | 0,0313 | ||
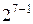
| 1,885 | 0,9000 | 0,0127 | 0,0141 | 0,0389 | 0,0156 | ||
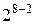
| 2,001 | 0,8889 | 0,0123 | 0,0139 | 0,0312 | 0,0156 |
 2015-05-13
2015-05-13 919
919







