
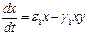
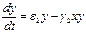

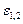 – коэффициенты врожденной скорости роста численностей;
– коэффициенты врожденной скорости роста численностей; 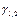 –коэффициенты чувствительности к недостатку корма.
–коэффициенты чувствительности к недостатку корма.
Найдем координаты особой точки
e1х - g1хy = 0; x×(e1 - - g1y) = 0 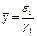
e2у+ g2хy = 0 y×(e2 + g2х) = 0 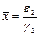
Т.к. все параметры положительны, точка 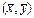 расположена в положительном квадранте фазовой плоскости.
расположена в положительном квадранте фазовой плоскости.
Т.к. запасы пищи не безграничны, то выедание ее приведет к голоданию и, это естественно предположить, к уменьшению скоростей роста популяций. Пусть 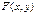 -количество пищи, съедаемой представителями обоих видов за единицу времени. Характер этой функции ясен. Она должна стремиться к плюс бесконечности при неограниченном росте хотя бы одного аргумента и стремиться к нулю, когда оба аргумента стремятся к нулю. В простейшем случае можно положить:
-количество пищи, съедаемой представителями обоих видов за единицу времени. Характер этой функции ясен. Она должна стремиться к плюс бесконечности при неограниченном росте хотя бы одного аргумента и стремиться к нулю, когда оба аргумента стремятся к нулю. В простейшем случае можно положить:
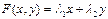 , l
, l 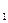 >0,l
>0,l  >0
>0
С увеличением 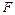 уменьшаются скорости роста популяций. Таким образом получим систему:
уменьшаются скорости роста популяций. Таким образом получим систему:
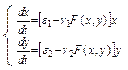
 (1.1)
(1.1)
Коэффициенты 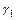 и
и 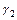 называются коэффициентами чувствительности к недостатку корма. Будем считать функцию
называются коэффициентами чувствительности к недостатку корма. Будем считать функцию 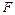 достаточно гладкой (т.е. имеющей достаточно большое число производных). Поэтому система (4.1) удовлетворяет условиям теоремы о существовании единственности решения задачи Коши:
достаточно гладкой (т.е. имеющей достаточно большое число производных). Поэтому система (4.1) удовлетворяет условиям теоремы о существовании единственности решения задачи Коши:
|
|
|
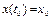 ,
, 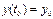
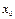 и
и 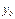 - это значения численности видов в начальный момент времени.
- это значения численности видов в начальный момент времени.
Чтобы выяснить дальнейшие свойства решения системы (4) найдем ее первый интеграл. Для этого запишем систему:
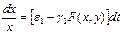
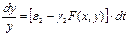
Умножим первое на 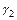 , а второе на
, а второе на 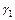 и вычтем из первого второе
и вычтем из первого второе
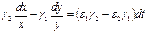
Интегрируем:
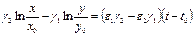
x,y –численности популяций в момент времени t; t0=0.
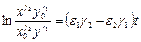
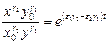
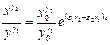 (1.2)
(1.2)
Случай 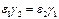 мало вероятен, поэтому не рассматривается.
мало вероятен, поэтому не рассматривается.
1. Пусть 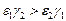 , тогда
, тогда
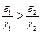 (1.3)
(1.3)
Тогда показатель у экспоненты в (4.2) будет положительным и при 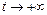 получим:
получим:
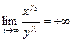
Так как 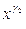 ограничена, то последнее равенство может выполняться только тогда, когда
ограничена, то последнее равенство может выполняться только тогда, когда 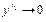 при
при 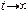 .
.
Если справедливо неравенство (1.3), т.е., если у второго вида скорость роста 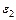 меньше и чувствительность к недостатку корма
меньше и чувствительность к недостатку корма 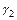 больше, чем у первого вида, то второй вид с течением времени исчезает. Можно показать, что первый вид при этом стабилизируется, т.е. численность
больше, чем у первого вида, то второй вид с течением времени исчезает. Можно показать, что первый вид при этом стабилизируется, т.е. численность 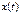 стремится к некоторому отличному от нуля числу. Покажем это для простейшей функции:
стремится к некоторому отличному от нуля числу. Покажем это для простейшей функции: 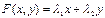 ,
, 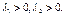
Т.к. 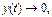 при
при 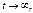 то начиная с некоторого момента
то начиная с некоторого момента 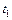 величина
величина 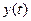 станет столь малой, что ею можно пренебречь и вместо
станет столь малой, что ею можно пренебречь и вместо 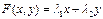 в первом уравнении можно записать
в первом уравнении можно записать 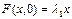 . Иными словами начиная с
. Иными словами начиная с 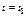 первое уравнение системы может быть записано в виде:
первое уравнение системы может быть записано в виде:
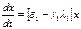
Это уравнение не отличается от уравнения логистического роста Ферхюльста- Перла. Его решение, при 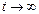 стремится к постоянной величине равной отношению коэффициентов
стремится к постоянной величине равной отношению коэффициентов 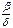 , данном случае
, данном случае 
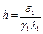 . Таким образом, при
. Таким образом, при 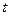
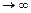 функция
функция 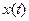 стабилизируется, стремясь к
стабилизируется, стремясь к 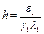 .
.
Итак, при любых начальных данных вид у которого отношение 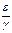 больше, выживает и стабилизируется; вид с меньшим отношением
больше, выживает и стабилизируется; вид с меньшим отношением 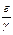 вымирает.
вымирает.
|
|
|
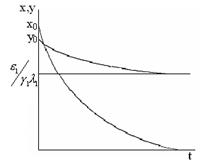
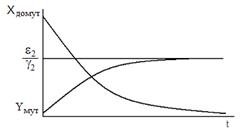
На рисунке изображен случай, когда начальная численность для 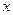 больше предельного значения
больше предельного значения 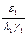 .Это совершенно необязательно. Из доказанного следует, что первый вид выживает и стабилизируется, каким бы малым ни было начальное значение
.Это совершенно необязательно. Из доказанного следует, что первый вид выживает и стабилизируется, каким бы малым ни было начальное значение 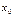 , а второй вид погибнет, сколь бы ни была велика его численность в начальный момент
, а второй вид погибнет, сколь бы ни была велика его численность в начальный момент 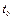 .
.
Теперь представьте себе, что у нас имеется только один вид (однородный штамм) с некоторым отношением 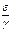 . В какой-то момент
. В какой-то момент 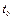 случайно появляется мутант с новым отношением
случайно появляется мутант с новым отношением 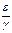 больше прежнего. Тогда, согласно нашей теории, сколь бы мало ни было мутантов в начальный момент, со временем они вытеснят домутантную форму, а сами стабилизируются.
больше прежнего. Тогда, согласно нашей теории, сколь бы мало ни было мутантов в начальный момент, со временем они вытеснят домутантную форму, а сами стабилизируются.
 2015-05-13
2015-05-13 631
631








