Краткие теоретические сведения. к выполнению лабораторных работ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению лабораторных работ

по дисциплине «МОДЕЛИРОВАНИЕ»

для студентов направления

«Компьютерная инженерия»

дневной формы обучения

Часть 1

МАРКОВСКИЕ ЦЕПИ.

Аналитические модели

Систем массового обслуживания

Севастополь

УДК 65.012 (075.8)

Методические указания к выполнению лабораторных работ по дисциплине «Моделирование» для студентов направления «Компьютерная инженерия» дневной формы обучения. Часть1/ Сост. В.В. Кирюхин, Е.Н. Мащенко – Севастополь, Изд-во СевНТУ, 2009. – 28 c.

Целью методических указаний является оказание помощи студентам в освоении методов построения моделей с использованием теории марковских цепей и теории массового обслуживания.

Методические указания рассмотрены и утверждены на заседании кафедры кибернетики и вычислительной техники, протокол № 8 от 24.04.09 г.

Рецензент: Шушляпин Е.А., доктор технических наук, профессор кафедры технической кибернетики

Допущено учебно-методическим центром СевНТУ в качестве методических указаний.

Содержание

		Стр
	Лабораторно-практическое занятие № 1. Дискретные и непрерывные марковские цепи
	Лабораторно-практическое занятие № 2. СМО с отказами. СМО с очередями
	Лабораторно-практическое занятие № 3. СМО с многомерным входящим потоком. СМО с относительными приоритетами
	Лабораторно-практическое занятие № 4. СМО с абсолютными и смешанными приоритетами
	Библиографический список

Лабораторно-практическое занятие № 1.

Дискретные и непрерывные марковские цепи

Цель занятия

Цель занятия - освоить методику построения моделей вычислительных систем с помощью аппарата дискретных и непрерывных марковских цепей; научиться строить марковские цепи по содержательному описанию задачи; научиться доказывать неприводимость цепи, находить вероятности состояний системы на некотором шаге, а также финальные вероятности.

Краткие теоретические сведения

Случайный процесс 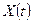называется марковским, если для любого момента времени 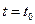вероятность любого его состояния (значения) в момент 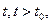зависит только от его состояния в момент 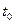и не зависит от всех состояний при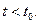

Если 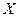принимает дискретные значения (состояния) 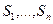, то марковский процесс называется марковской цепью.

Марковская цепь называется однородной, если её свойства, как случайного процесса, не зависят от сдвигов по оси времени. (Свойство однородности цепи соответствует свойству стационарности общего случайного процесса).

Рассмотрим дискретную однородную марковскую цепь с конечным числом состояний (значений) S₁, …, S_n.. Переходы из состояния в состояние происходят только в дискретные моменты t=0,1,2,…. Промежутки между такими моментами называются тактами; такты нумеруются так же, как и моменты, т.е. моменту 0 соответствует такт 0, и т.д.

Как случайный процесс, такая цепь полностью определяется вектором p(k) распределения вероятностей состояний в момент k:

p(k)=(p₁(k),…, p_i(k), …,p_n(k)),

где p_i(k) - вероятность того, что цепь в момент k находится в состоянии S_i.

Для k =0,1,… имеет место равенство:

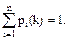(1.1)

Для вычисления любого p(k) достаточно знать всего два объекта: вектор p(0)=(p₁(0), …, p_i(0), …, p_n(0)) начального распределения вероятностей состояний и матрицу

,

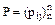где p_ij - вероятность перехода цепи из S_i в S_j за один такт.

Связь между векторами p(k) и p(k-1) устанавливается по формуле

p(k)=p(k-1)Р. (1.2)

Эта формула, в частности, позволяет по известным р(0) и Р вычислить р(1), по р(1) и Р определить р(2) и т.д., вплоть до произвольного p(k).

Марковская цепь называется неприводимоймарковской цепью, если из любого её состояния можно перейти в любое другое состояние за конечное число тактов.

Для неприводимой марковской цепи существуют пределы:

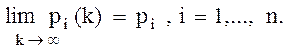(1.3)

Числа р_i называются финальными вероятностями состояний цепи; соответственно вектор р=(р₁, …, р_i,…, р_n) называется вектором финальных вероятностей.

Вектор финальных вероятностей можно найти, полагая в формуле (1.2) p(k)=p(k-1)=р и рассматривая полученное таким образом соотношение как уравнение относительно р. К этому уравнению необходимо добавить условие нормировки (1.1), где p(k)=р.

В результате получим систему уравнений для отыскания финальных вероятностей:

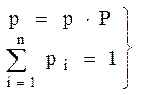. (1.4)

Финальные вероятности состояний существуют и для непрерывных марковских цепей, только необходимо учитывать специфику, создаваемую фактом континуальности времени. Именно, здесь неприводимая цепь определяется как цепь, в которой из любого состояния можно перейти в любое другое за конечное время (а не за конечное число тактов); далее, матрица Р здесь заменяется на матрицу

,

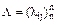где l_ij - интенсивность переходов цепи из состояния S_i в S_j, имеющая смысл среднего количества переходов за единицу времени.

Сами финальные вероятности p_i определяются как

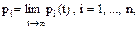(1.5)

где p_i(t) - вероятность пребывания цепи в состоянии S_i в момент t.

Компоненты p_i вектора (р₁,…,p_n) финальных вероятностей вычисляются как корни системы уравнений Колмогорова:

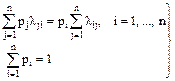. (1.6)

В заключение заметим, что в системах (1.4) и (1.6) одно из первых n алгебраических уравнений является избыточным, и перед решением системы его (обычно самое громоздкое) необходимо удалить.