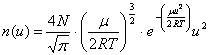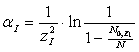|
В природе, в жизни, в технике часто наблюдаются случайные явления. Предсказать отдельные случайные явления нельзя, так как на них сказывается влияние очень большого числа не поддающихся контролю факторов. Например, при стрельбе в цель, при измерении физических величин, при движении молекул и т.п. в той или иной степени наблюдаются несколько элементов случайности. Однако, даже если можно было бы учесть определяющие данное явление факторы, то одно единичное явление ещё не характеризует общей картины случайных явлений. Например, одно наугад выбранное отверстие в мишени ничего не говорит нам о меткости стрелка, в то время как большое число произведенных выстрелов дает понятие о точности стрельбы в цель.
Случайные явления наиболее полно описываются при помощи математического аппарата теории вероятностей. Большая совокупность случайных явлений или величин подчиняются статистическим законам. Статистические законы дают возможность определять вероятность, с которой осуществляется то или иное событие в серии измеряемых величин, наиболее вероятные отклонения от среднего и т.п. Все эти характеристики определяются законом распределения случайных величин - зависимостью вероятности появления данной величины от значения самой величины.
Наиболее распространенным в природе законом распределения случайных величин является закон нормального распределения (закон Гаусса). Это распределение имеет место в том случае, если случайная величина зависит от большого числа факторов, которые вносят с равной вероятностью положительные и отрицательные отклонения. Примером такого распределения может служить распределение случайных ошибок при изменении любой физической величины. Действительно, на величину полученного результата измерения влияют такие факторы, как нестабильность физических условий (например, температуры), при которых проводились измерения, случайные колебания прибора, различные положения глаза при отсчете показаний прибора, индивидуальные свойства глаза наблюдателя и т.д. Ошибку каждого измерения можно разбить на более мелкие элементарные ошибки, вызванные различными причинами, предположив, что они имеют одинаковую величину и равновероятные знаки.
Число измерений 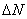 , давших отклонение от среднего значения измеряемой величины в пределах от , давших отклонение от среднего значения измеряемой величины в пределах от 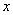 до до 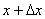 , пропорционально интервалу , пропорционально интервалу 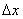 и полному числу измерений N. Функция и полному числу измерений N. Функция 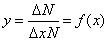 называется законом распределения или плотностью вероятности. Можно показать, что закон нормального распределения (закон Гаусса) имеет вид называется законом распределения или плотностью вероятности. Можно показать, что закон нормального распределения (закон Гаусса) имеет вид
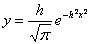
где
x - отклонение измеряемой величины от ее среднего значения,
у - плотность вероятности появления ошибки величины,
h - мера точности.
Вывод закона нормального распределения
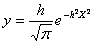 . .
Пусть в каждое измерение входит 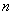 элементарных ошибок равной величины элементарных ошибок равной величины 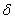 , каждая из которых с равной вероятностью , каждая из которых с равной вероятностью 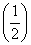 может иметь положительный и отрицательный знак. Вероятность того, что все может иметь положительный и отрицательный знак. Вероятность того, что все  , элементарных ошибок войдут в измерение со знаком "+", равна , элементарных ошибок войдут в измерение со знаком "+", равна 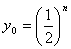 т.е. произведению вероятностей каждого из n событий. Результирующая ошибка в этом случае равна т.е. произведению вероятностей каждого из n событий. Результирующая ошибка в этом случае равна 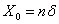 . Вероятность такого события, когда . Вероятность такого события, когда 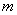 элементарных ошибок из элементарных ошибок из 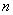 имеют отрицательные знаки, а остальные (n-m) - положительные знаки, равна имеют отрицательные знаки, а остальные (n-m) - положительные знаки, равна
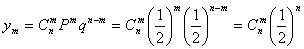
где 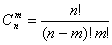 - число возможных сочетаний из n ошибок по числу отрицательных ошибок m. - число возможных сочетаний из n ошибок по числу отрицательных ошибок m.
Величина соответствующей результирующей ошибки 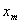 будет равна будет равна 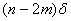 . Представим это в виде таблицы(см. табл.1). . Представим это в виде таблицы(см. табл.1).
Зависимость вероятности появления ошибки y от величины x представляет собой ступенчатую кривую. При уменьшении элементарных ошибок d при вероятности их числа n так, чтобы 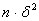 стремилась к конечному пределу, ступенчатая кривая приближается к плавной. Найдем аналитическое выражение этого распределения при стремилась к конечному пределу, ступенчатая кривая приближается к плавной. Найдем аналитическое выражение этого распределения при  . .
Таблица № 1
Число элементарных ошибок |
Результирующая ошибка
|
Вероятность появления такой ошибки
|
положительн.
|
отрицат.
|
n
|
0
|
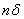
|
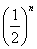
|
n-1
|
1
|
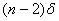
|
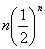
|
n-m
|
m
|
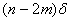
|
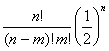
|
n-m-1
|
m+1
|
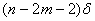
|
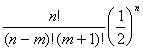
|
Касательная к кривой определяется пределом отношения  при при  : :
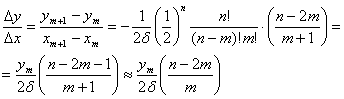
так как 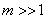 . .
Поскольку 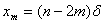 , то , то 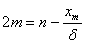 и и

При  будем иметь, что будем иметь, что  стремится к постоянному пределу, который обозначим стремится к постоянному пределу, который обозначим 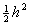 , отсюда , отсюда
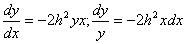
Интегрируя, получим выражение
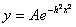 . .
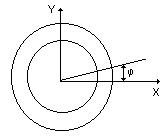
Рис. 1
|
Другим примером распределения случайных отклонений может служить стрельба в цель. Большое число неподдающихся контролю факторов (неточность прицела, несимметричность пули, дефекты ружья и т.п.) приводят к случайным отклонениям пули от цели. Однако, в данном случае элементарные ошибки имеют не два равно-вероятных значения (положительное и отрицательное), а бесконечное множество значений, соответствующих смещениям точки попадания по различным радиусам в плоской мишени.
Вдоль любого направления j , проведенного через максимум плотности попадания, закон имеет характер нормального распределения 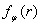 (см. рис. 2). Если же нас интересует вероятность отклонения от цели на расстояние r независимо от направления, то плотность вероятности попадания (см. рис. 2). Если же нас интересует вероятность отклонения от цели на расстояние r независимо от направления, то плотность вероятности попадания 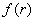 надо просуммировать, по площади кольца радиусом r и шириной надо просуммировать, по площади кольца радиусом r и шириной 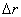 . .
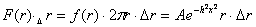
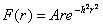
В результате одномерный закон распределения отклонений от цели приобретает вид ассиметричного максимума, смещенного относительно центра (см. рис. 3)
Аналогичная картина наблюдается и при изучении распределения молекул газа по скоростям - распределения Максвелла. Случайные столкновения молекул газа при их хаотическом движении приводят к случайным изменениям их скорости как по величине, так и по направлению. Если рассматривать распределение молекул по скоростям вдоль какого-нибудь одного направления,
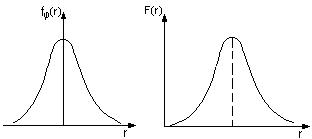 Рис. 2 Рис. 3 Рис. 2 Рис. 3
то большое число случайных соударений приводит к закону нормального распределения вдоль этого направления. Если же интересоваться числом молекул 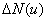 , имеющих скорости в интервале от u до u+ , имеющих скорости в интервале от u до u+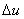 независимо от направления, то необходимо просуммировать закон нормального распределения по всем направлениям в пространстве. Тогда: независимо от направления, то необходимо просуммировать закон нормального распределения по всем направлениям в пространстве. Тогда:
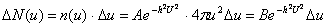
Пронормировав это выражение, получим:
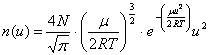
где m - молекулярный вес;
R - универсальная газовая постоянная;
N - общее число молекул.
Из последнего уравнения видно, что закон распределения молекул газа по скоростям качественно имеет такой же характер, как и при стрельбе в цель.
Для ознакомления с законами распределения, аналогичными закону Максвелла (закону распределения молекул по скоростям), служит механическая модель, осуществляющая двумерное рассеяние частиц.
Целью данной работы является изучение статистического закона распределения,
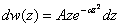 , (1) , (1)
в котором 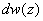 - вероятность получения значений z в интервале - вероятность получения значений z в интервале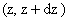 , А и , А и 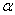 - постоянные. Здесь экспериментальная проверка закона (1) основывается на изучении распределения радиальных отклонений зерен. Зерно, просыпаясь через сетки, рассеивается по всем направлениям в плоскости, параллельной плоскостям сеток и образует распределение, подобное распределению точек попадания пуль при стрельбе в мишень. - постоянные. Здесь экспериментальная проверка закона (1) основывается на изучении распределения радиальных отклонений зерен. Зерно, просыпаясь через сетки, рассеивается по всем направлениям в плоскости, параллельной плоскостям сеток и образует распределение, подобное распределению точек попадания пуль при стрельбе в мишень.
Выбор не трехмерного распределения Максвелла, имеющего вид
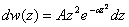 , (2) , (2)
а двумерного распределения, оправдан не только значительной простотой его осуществления, но и тем, что формула (1) обладает, всеми существенными особенностями формулы (2). Например, в обоих случаях с увеличением z наблюдается возрастание функции
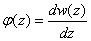 (плотность вероятности) при малых z и её асимптотическое стремление в "О" при больших z. (плотность вероятности) при малых z и её асимптотическое стремление в "О" при больших z.
При выполнении работы используются формулы
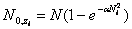 (3) (3)
и
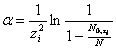 , (4) , (4)
которые легко получить интегрированием формулы (1), если произвести её нормировку и переписать в виде
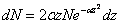 , (5) , (5)
где
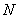 - общее число зерен, подвергавшихся испытанию; - общее число зерен, подвергавшихся испытанию;
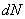 - число зерен, радиальные отклонения которых лежат в интервале (z,z+dz); - число зерен, радиальные отклонения которых лежат в интервале (z,z+dz);
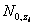 - число зерен, отклонения которых лежат в интервале ( - число зерен, отклонения которых лежат в интервале (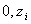 ). ).
Описание установки
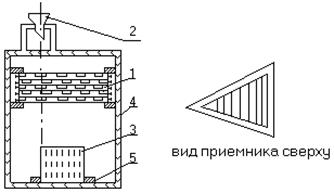
рис.4
Основной частью установки является стопка 1, составленная из 22 сеток (сит), расположенных друг над другом. Точки пересечения нитей каждой из сеток находятся над центрами квадратных ячеек её нижнего или верхнего соседа. Параметр ячеек равен 7 мм. Сквозь эту стопку через воронку 2 пропускается вертикальная струя зерен пшена. В результате рассеивания зерна попадают в различные отделения приёмника 3. Приёмник имеет вид призмы, в основании которой лежит равнобедренный треугольник с углом в 45° при вершине. Эта призма разделена плоскими перегородками, отстоящими друг от друга на расстоянии 2 см и параллельными её бедрам. С трех сторон стопка из сеток прикреплена к стенкам шкафа 4 . В основании шкафа имеется гнездо 5 , в котором устанавливается приемник. Расположение гнезда согласовано с положением воронки таким образом, что направление ребра приемника совпадает с осью воронки.
Выполнение работы.
1. На технических весах взвешивается I кг пшена.
2. Приемник с отделениями, закрытыми снизу пробками, помещается в гнездо. Закрывается дверца шкафа, а пшено засыпается в воронку.
3.Из шкафа извлекается приемник, поочередно открываются его отделения и взвешиванием на технических весах устанавливаются массы:
 зерен, рассеянных в углу, равном 45° в интервалах (0,2), (2,4),…,(12,14); границы интервалов даны в сантиметрах. зерен, рассеянных в углу, равном 45° в интервалах (0,2), (2,4),…,(12,14); границы интервалов даны в сантиметрах.
4. Опыт проводится не менее трех раз. Полученные данные записываются в таблицу.
Обработка результатов измерений
1. Так как данный приемник составляет примерно 1/8 часть цилиндрического приемника, который мы не берем, то необходимо массу зерен в каждом отделении приемника умножить на 8. По полученным данным строится гистограмма (M,Z), подобная которой показана на рис. 5.
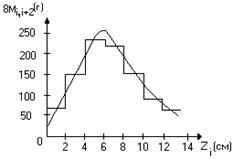
Рис. 5
2. Определить числа 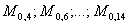
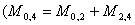 и т.д.) Так как отношение и т.д.) Так как отношение 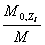 равно величине равно величине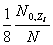 , то формула (4) переписывается в виде: , то формула (4) переписывается в виде:
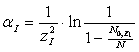
По этой формуле вычисляют значения 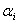 , соответствующие каждому из полученных значений , соответствующие каждому из полученных значений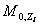
3. Затем вычисляется среднее значение и среднее отклонение
 . .
4. Если закон распределения (5), согласно которому 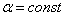 , действительно применим к реально протекающему процессу рассеяния, то средний разброс , действительно применим к реально протекающему процессу рассеяния, то средний разброс 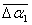 должен быть меньше средней экспериментальной погрешности должен быть меньше средней экспериментальной погрешности 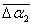 в округлении величины в округлении величины 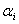 . Для проверки вычисляются значения . Для проверки вычисляются значения 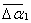 и и 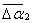 и сравниваются между собой. и сравниваются между собой.
|

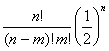
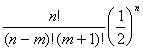
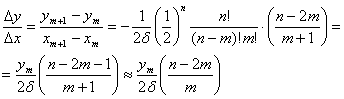

 Рис. 2 Рис. 3
Рис. 2 Рис. 3