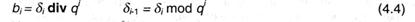Пример 4.1
Выполнить преобразование 223 → Z6. Последовательность действий и промежуточные результаты для наглядности представим в виде таблицы:
Следовательно, 223 = 126. Преобразование Zp → Z10 → Zq Очевидно, первая и вторая часть преобразования не связаны друг с другом, что дает основание рассматривать их по отдельности. Алгоритмы перевода Z10 → Zq вытекают из следующих соображений. Многочлен (4.1) для Zq может быть представлен в виде:
* Такое представление называется схемой Горнера. где т - число разрядов в записи Zq, а bj (j = 0...m - 1) - цифры числа Zq.
Разделим число Zq на две части по разряду номер i; число, включающее т - i разрядов с т - 1 -го по i-й обозначим γi, а число с i разрядами с i - 1-го по 0 -й - δi. Очевидно, i
Аналогично, если принять δ0 = b0, то для правой части числа будет справедливо другое рекуррентное соотношение: δi = δi-1 + bi ∙qi, из которого следуют:
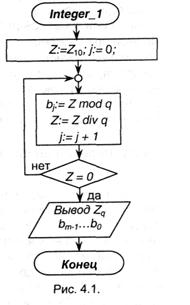
Из соотношении (4.3) и (4.4) непосредственно вытекают два способа перевода целых чисел из 10-ной системы счисления в систему с произвольным основанием q. Способ 1 является следствием соотношений (4.3), из которых просматривается следующий алгоритм перевода: 1) целочисленно разделить исходное число (Z10) на основание новой системы счисления (q) и найти остаток от деления - это будет цифра 0-го разряда числа Zq; 2) частное от деления снова целочисленно разделить на q с выделением остатка; процедуру продолжать до тех пор, пока частное от деления не окажется меньше q; 3) образовавшиеся остатки от деления, поставленные в порядке, обратном порядку их получения, и представляют Zq. Блок-схема алгоритма представлена на рис.4.1. Обычно его представляют в виде «лестницы».
|


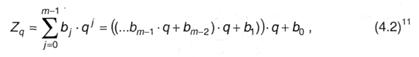
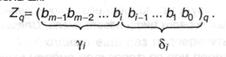
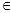 [0, т - 1], γ0 = δm-1 = Zq. Позаимствуем из языка PASCAL обозначение двух операций: div - результат целочисленного деления двух целых чисел и mod - остаток от целочисленного деления (13 div 4 = 3; 13 mod 4 = 1). Теперь если принять γm-1 = bm.1, то в (4.2) усматривается следующее рекуррентное соотношение: γi = γi+1 ∙ q + bi, из которого, в свою очередь, получаются выражения:
[0, т - 1], γ0 = δm-1 = Zq. Позаимствуем из языка PASCAL обозначение двух операций: div - результат целочисленного деления двух целых чисел и mod - остаток от целочисленного деления (13 div 4 = 3; 13 mod 4 = 1). Теперь если принять γm-1 = bm.1, то в (4.2) усматривается следующее рекуррентное соотношение: γi = γi+1 ∙ q + bi, из которого, в свою очередь, получаются выражения: