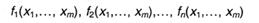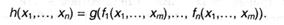Рекурсивные функции

Для дальнейшего рассмотрения нам понадобится ряд определений. Пусть имеются два множества X и Y.

Если некоторым элементам множества X поставлены в соответствие однозначно определенные элементы множества Y, то говорят, что задана частичная функцияиз X в Y.

Совокупность тех элементов множества X, у которых есть соответствующие элементы в Y, называется областью определения функции,а совокупность тех элементов Y, которые соответствуют элементам X, называются совокупностью значений функции.

Если область определения функции из X в Y совпадает с множеством X, то функция называется всюду определенной.

Исходная идея построения точного определения алгоритма, опирающегося на понятие рекурсивной функции, состоит в том, что любые данные (безусловно, дискретные) можно закодировать натуральными числами в некоторой системе счисления, и тогда всякое их преобразование сведется к последовательности вычислительных операций, а результат обработки также будет представлять собой целое число. В данном подходе любой алгоритм, единый для данной числовой функции, вычисляет ее значение, а его элементарными шагами оказываются обычные арифметические и логические операции. Такие функции получили название вычислимых.

Пусть имеется класс функций типа у(х_1, х₂, ..., х_п), особенностями которых является то, что все аргументы функции х₁,..., х_п целочисленны, и значение функции у также выражается целым числом. Другими словами, рассматриваются функции, аргументы и значения которых дискретны.

Функция у(x₁, х₂, ..., х_п) называется эффективно вычислимой, если существует алгоритм, позволяющий вычислить ее значение по известным значениям аргументов.

Поскольку понятие алгоритма в этом определении берется в интуитивном смысле, то и понятие эффективно вычислимой функции оказывается интуитивным. Тем не менее, при переходе от алгоритмов к вычислимым функциям возникает одно очень существенное обстоятельство. Совокупность процессов, удовлетворяющих условиям 1 - 5 из п. 7.1 и, следовательно, подпадающих под интуитивное понятие алгоритма, весьма обширна и мало обозрима. Напротив, совокупность вычислимых функций для самых разных пониманий процессов, удовлетворяющих перечисленным условиям, оказалась одной и той же и притом легко описываемой в обычных математических терминах. Эта точно описанная совокупность числовых функций, совпадающая с совокупностью всех вычислимых функций при самом широком до сих пор известном понимании алгоритма, носит название совокупности рекурсивных функций.

Любая алгоритмическая модель и, в том числе, рекурсивные функции, должна предусматривать определение элементарных шагов алгоритма и способов построения из них какой-то последовательности преобразований, обеспечивающих необходимую последовательность обработки данных. В рекурсивной модели такими «элементарными шагами» являются так называемые простейшие числовые функции S¹, 0ⁿ и I_mⁿ комбинацией которых строятся все более сложные и которые определяются следующим образом:

· S¹(x) = х + 1 - это одноместная (т.е. имеет один аргумент) функция непосредственного следования;

· 0ⁿ(х₁, х₂.....x_n) = 0 - это n-местная функция, тождественного равенства нулю;

· I_mⁿ(x₁,.....x_n) = x_m (1 ≤ т ≤ n; n = 1, 2, ...) - п-местная функция тождественного повторения значения одного из своих аргументов.

Перечисленные простейшие функции всюду определены и интуитивно вычислимы. Над ними определяются операции (в дальнейшем они называются операторами), обладающие тем свойством, что их применение к функциям, вычислимым в интуитивном смысле, порождает новые функции, также заведомо вычислимые в интуитивном смысле. Частичные функции, которые можно получить при помощи этих операторов из простейших функций называются частично рекурсивными. Гипотеза Черча состоит в том, что класс построенных таким образом частично рекурсивных функций совпадает с классом функций, допускающим алгоритмическое вычисление.

Переходим к рассмотрению операторов, обеспечивающих преобразование простейших функций.

Суперпозиция частичных функций

Пусть m-местные функции

подставляются в n-местную функцию g(x₁,..., x_n). В результате получается n-местная функция

Говорят, что функция h получена из функций g, f₁, ..., f_n суперпозицией (или подстановкой). Символически такая подстановка обозначается следующим образом: Sⁿ⁺¹(g, f₁, ..., f_n), где индекс сверху обозначает количество функций, подставляемых в качестве аргументов.

Если умеем вычислять функции g, f₁, ..., f_n, то функция h также может быть вычислена. Ясно также, что если все функции g, f₁, ..., f_n всюду определены, то и функция h также всюду определена. Таким образом, если функции g, f₁, ..., f_n интуитивно вычислимы, то будет интуитивно вычислимой и функция h.