ЛИНИИ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ К ПЛОСКОСТЯМ ПРОЕКЦИЙ
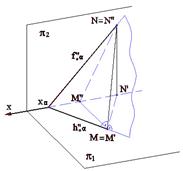
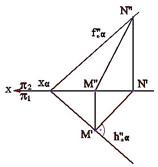
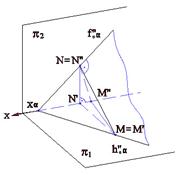
Прямая, лежащая в плоскости общего положения и перпендикулярная к линии уровня или следу плоскости, называется линией наибольшего наклона плоскости к соответствующей плоскости проекций. Линии наибольшего наклона плоскости a к горизонтальной и фронтальной плоскостям проекций показаны на рис.3.9а и 3.9б, 3.10а и 3.10б.
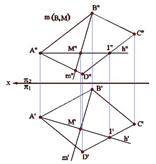
Рис.3.9а Рис.3.9б Рис.3.10а Рис.3.10б На рис.3.11приведен пример линии наибольшего наклона плоскости, заданной плоской фигурой - параллелограммом АВСD (линия m) - по отношению к горизонтальной плоскости проекций p1. Построение ясно из чертежа.
Рис.3.11 Поскольку линия наибольшего наклона перпендикулярна соответствующей линии уровня данной плоскости, то очевидно, что с помощью только одной линии - линии уровня плоскости по отношению к той или иной плоскости проекций, можно задать плоскость общего положения в пространстве. На рис.3.12 плоскость b задана линией наибольшего наклона к фронтальной плоскости проекций - линией n. Второй линией в этом случае является линия фронтали f, которую можно провести через любую точку линии l наибольшего наклона данной плоскости.
Рис. 3.12 Литература: Гордон В.О. и др. Курс н.г., 1988: с. 32-37; 42-49;62-64. Фролов С.А. Н.г., 1983.: с.34-42. |