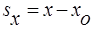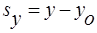Различают скалярные и векторные величины.
Скалярные величины – величины, характеризующиеся числовым значением (t¸ m). Векторные величины – величины, характеризующиеся числовым значением и направлением (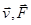 ).
).
Сложение векторов. Вектора складываются по правилам:
1) параллелограмма – расположить вектора 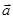 и
и 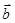 так, чтобы они выходили из одной точки, достроить до параллелограмма; диагональ, исходящая из начальной точки и является суммой этих векторов;
так, чтобы они выходили из одной точки, достроить до параллелограмма; диагональ, исходящая из начальной точки и является суммой этих векторов;
2) треугольника – из конца вектора 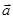 отложить вектор
отложить вектор 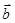 ; вектор, соединяющий начало вектора
; вектор, соединяющий начало вектора 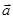 и конец вектора
и конец вектора 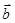 , является суммой этих векторов.
, является суммой этих векторов. 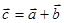
Математические действия с векторами производятся геометрически.
Если вектора параллельны, то они складываются аналогично. По модулю результирующий вектор равен арифметической сумме (если в одну сторону), либо арифметической разности (если в разные стороны). Направлен результирующий вектор либо в ту же сторону, что и складываемые векторы, либо в сторону большего по модулю вектора.
Проекцией вектора 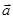 на ось Х называется отрезок
на ось Х называется отрезок 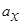 между проекциями на эту ось начала и конца вектора. Если проекция вектора на ось совпадает с положительным направлением оси, то она положительна. В противном случае проекция вектора отрицательна. Если вектор перпендикулярен оси, то его проекция на ось равна нулю.
между проекциями на эту ось начала и конца вектора. Если проекция вектора на ось совпадает с положительным направлением оси, то она положительна. В противном случае проекция вектора отрицательна. Если вектор перпендикулярен оси, то его проекция на ось равна нулю.
Проекция вектора на ось – скаляр, поэтому математические действия с проекциями производятся алгебраически.
Если известен вектор перемещения, то известна и его проекция на координатную ось (или оси). Рассмотрим это на примере. Пусть тело совершило перемещение 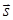 , где (
, где (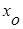 ,
, 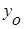 ) – начало перемещения, (x,y) – конец перемещения.
) – начало перемещения, (x,y) – конец перемещения.
|
- проекция вектора 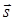 на ось Х
на ось Х
|
- проекция вектора 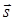 на ось Y
на ось Y
Проекция вектора перемещения 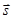 на оси координат X и Y равны изменениям координат тела x и y.
на оси координат X и Y равны изменениям координат тела x и y.
Зная вектор перемещения, можно узнать и координаты тела x и y:
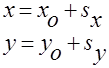
Модуль вектора перемещения равен 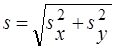
Если треугольник не прямоугольный, то одну из сторон можно найти по теореме косинусов: a2= b2 + c2 – 2bс cos α
 2015-05-26
2015-05-26 398
398