2015-05-26
1311
Рассмотрим две бесконечные параллельные разноименно заряженные плоскости. Пусть создаваемое ими в вакууме поле характеризуется напряженностью Е0 =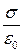 
, где σ – поверхностная плотность сторонних зарядов, которые находятся за пределами диэлектрика. Внесем в это поле пластину из однородного изотропного диэлектрика и расположим ее так, как показано на рис.17.15. Под действием поля диэлектрик поляризуется, и на его поверхностях появятся связанные заряды плотности 
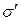. Эти заряды создадут внутри пластины однородное поле, напряжённость которого равна Е'= 
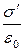. Поляризация диэлектрика обусловлена полем внутри диэлектрика
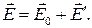(17.27)
 |
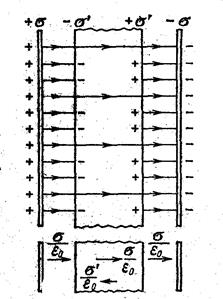Рис.17.15. Поле в диэлектрике
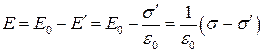, (17.28)
так как поля сторонних и связанных зарядов направлены навстречу друг другу.
Нам известно, что напряженность поля в диэлектрике, находящемся в плоском конденсаторе, при поверхностной плотности сторонних зарядов σ равна
= 
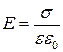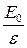. (17.29)
Из формул (17.28-17.29) следует, что - поскольку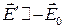 
- поле в диэлектрике ослабляется в ε раз. В рассматриваемом случае диэлектрическая проницаемость 
показывает, во сколько раз ослабляется поле.
|
|
|
Плотность связанных зарядов оказывается всегда меньше плотности сторонних зарядов, создающих в процессе поляризации эти связанные заряды – в соответствии с формулой (17.28) -
-
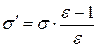- в противном случае поле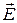 
в диэлектрике изменило бы знак по сравнению с полем 
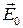, его создающим.
Величина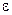 
, называемая диэлектрической проницаемостью, показывает отношение
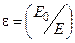. (17.30)
Ясно, что всегда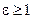 
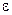( = I в вакууме).
Диэлектрическая проницаемость диэлектрика
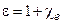,(17.31)
где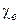 
- диэлектрическая восприимчивость диэлектрика.
Удельная поляризованность диэлектрика (вектор поляризации) равна
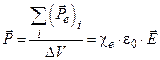.(17.32)
где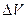 
- объем диэлектрика.
