Задачи. 1. Доказать принцип резолюции в ИВ

1. Доказать принцип резолюции в ИВ.

2. Доказать при помощи принципа резолюции невыполни-мость и построить соответствующие деревья вывода для множеств дизъюнктов:

а) {PÚQ, Ø PÚQ, PÚØQ, ØPÚØQ}; б) {PÚØQÚØR, ØPÚØR,

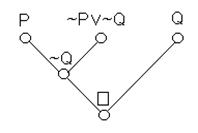
Рис.3.26

Q, R}; в) {ØPÚØQ, QÚØR, PÚ Ø Q, R}; г) {P, QÚR, ØPÚØR, ØQÚ R }; д) {PÚQÚR, ØPÚR, Ø Q, Ø R }, е) {PÚRÚQ, ØQ, ØPÚQ, ØR, ØPÚR}; ж) {S, ØPÚRÚØS, PÚØS, ØR,}.

6.5.2 Операции подстановки, унификации и склейки

В ИВ литеры дизъюнктов в конкретных интерпрета-циях являются логическими константами, поэтому поиск контрарных литер прост. В теориях первого порядка, где в качестве литер выступают предикаты, являющиеся логи-ческими функциями от констант, предметных переменных и функций, поиск контрарных литер усложняется.

Рассмотрим множество дизъюнктов S. Поскольку не-выполнимость S доказывается сразу для всех возможных интерпретаций, то для получения контрарных пар литер в дизъюнктах S (и, соответственно, получения резольвент) можно использовать дизъюнкты не только в их исходной форме, но и новые дизъюнкты, получаемые путём различ-ных подстановок в литеры вместо предметных переменных некоторых термов.

Пример 1. Доказать невыполнимость множества дизъ-юнктов S = {P(x) Ú Q(z,y), ØP(f(y)), Ø Q(z,a)}.

Решение. В исходных дизъюнктах контрарных пар литер нет. Подставив в первый дизъюнкт D₁ = P(x) Ú Q(z,y) вмес-то x функцию f(y), получаем новый дизъюнкт D^¢₁ = P(f(y)) Ú

Q(z,y), который имеет контрарную пару литер с дизъюнктом D₂ = Ø P(f(y)). Применяя правило резолюции к D^¢₁ и D₂, получим резольвенту D₄ = Q(z,y). Подставляя в D₄ вместо y константу a, получим пару контрарных дизъюнктов Ø Q(z,a) и Q(z,a). После применения к ним правила резолюции по-лучим резольвенту, равную пустому дизъюнкту ÿ, что до-казывает невыполнимость S.

Рассмотрим подстановки более подробно.

Определение. Подстановками называются конечные множества вида q = {t₁/x₁,..., t_n/x_n},

где (x₁,..., x_n) - попарно различные предметные переменные, (t₁,..., t_n) - термы, отличные от соответствующих пере-менных (при 1 £ i £ n: t_i ¹ x_i). Обозначаются подстановки буквами из греческого алфавита.

Определение. Пустой называется подстановка, не со-держащая замен: n=0. Обозначается пустая подстановка че-рез e.

Допустим, рассматривается некоторое множество дизъюнктов S = {D₁, D₂,..., D_k}.

Определение. Примером дизъюнкта D_i Î S назы-вается результат одновременной подстановки q ={t₁/x₁,..., t_n/x_n} термов (t₁,..., t_n) вместо переменных (x₁,..., x_n) в D_i. Обозначается данный пример как D_iq. Каждую подстановку {t_i/x_i} будем для краткости называть элементарной.

В отличие от ранее рассмотренных основных приме-ров дизъюнктов примеры могут содержать предметные пе-ременные, поскольку при подстановке они могут заменяться новыми предметными переменными, а также может произ-водиться только частичная их замена термами.

Пример 2. Применить к дизъюнкту D_i = P(x) Ú Q (f(y)) Ú ØR (z,a) подстановку q = {g(y)/x, a/y,x/z}.

Решение. После подстановки получаем пример следующего

вида: D^¢_i = P(g(y)) Ú Q (f(а)) Ú ØR (x,a).

Допустим, вначале к некоторому дизъюнкту D_i была применена подстановка q = {t₁/x₁,..., t_n/x_n}, после чего все переменные (x₁,..., x_n) были заменены термами (t₁,...,t_n). За-тем к вновь полученному дизъюнкту была применена под-становка l = {u₁/y₁,...,u_m/y_m}. В итоге её применения а) все переменные (y₁,...,y_m) были заменены термами (u₁,..., u_m), б) термы из (t₁,...,t_n), которые входят в множество (y₁,...,y_m), также были заменены термами (u₁,...,u_m). Результат второй подстановки обозначим через (t₁l,...,t_nl). При последова-тельном применении q, а затем l возможно появление тож-дественных элементарных подстановок, при которых t_il = x_i. Например, подстановка q, содержит элементарную под-становку {y/x}, а l - элементарную подстановку {х/y}. Тогда при последовательном применении q и l появится элемен-тарная тождественная подстановка {х/х}.

Если в подстановки q и l входят одинаковые пред-метные переменные x_i и y_j (x_i = y_j), то при второй подста-новке l элементарная подстановка u_j/y_j уже не будет “сра-батывать”, поскольку все элементы y_j уже будут заменены при первой подстановке.

Определение. Если первой была применена подста-новка q, а второй - подстановка l, то их композицией ( q°l) называется подстановка, выполняющая сразу те же замены, что и при данные подстановки при последовательном при-менении.

Утверждение. Композиция (q ° l) подстановок q = {t₁/x₁,..., t_n/x_n} и l ={u₁/y₁,...,u_m/y_m} может быть получена из подстановки { t₁l/x₁,..., t_nl/x_n , u₁/y₁,...,u_m/y_m} вычёркиванием:

а) всех элементарных подстановок t_il/x_i, у которых t_il = x_i (тождественных),

б) всех элементарных подстановок u_j/y_j, у которых y_j Î (x₁,..., x_n) (т.е. таких элементарных подстановок, которые не будут

применяться во второй подстановке l вследствие того, что элементы y_j уже изменены первой подстановкой q. Cпра-ведливость утверждения следует из сделанных выше заме-чаний.

Пример 3. Построить композицию (q°l) подстановок q = {у / x, z / y, f(a) / z} и l = {b / z, x / y}.

Решение. Так как уl = х, zl = b, а к f(a) подстановка l не применима, то

{ t₁l/x₁,..., t_nl/x_n , u₁/y₁,...,u_m/y_m} = { x/x, b/y, f(a)/z, b/z, x/y}.

Вычеркиваем первую элементарную подстановку х/x (тождественную), а также четвёртую и пятую b/z, x/y, кото-рые не участвуют во второй подстановке l из-за того, что переменные z, y изменены в первой подстановке. В итоге получим: (q ° l) = { b/y, f(a)/z}.