Семантические деревья. Теорема Эрбрана

Множества H(S), A¢, F¢, у всех Н - интерпретаций сов-падают. Различаются только значения предикатов, которые могут быть либо равны атомам из эрбрановского базиса А, либо противоположны им. Каждый атом А_i Î А входит в одну интерпретацию один раз - либо как А_i, либо как Ø А_i. Пара А_i и Ø А_i называется контрарной.

Рассмотрим для некоторого множества дизъюнктов S эpбрановский базис А = (А₁ , А₂ ,...).

Определение. Полным семантическим деревом Т(S) множества дизъюнктов S называется растущее вниз бинар-ное дерево, в котором из самой верхней вершины - корня (узел 0 -го уровня) выходит пара рёбер А₁ и ØА₁, из каждого узла i -го уровня - пара рёбер А_i и Ø А_i.

Определение. Путь, включающий в себя по одному узлу каждого уровня i (i =0,1,2,...), называется ветвью.

Очевидно, при счетном эрбрановском базисе число уровней дерева Т(S) и длина ветвей в нем (число узлов) счетны. Каждая ветвь в Т(S) задаёт одну Н – интерпре-тацию, а все дерево описывает полное множество Н -интер-претаций множества дизъюнктов S.

Пример 1. Построить полное семантическое дерево Т(S) для множества дизъюнктов S = {P(x) Ú Q(f(x)), P(a) Ú Q(y)}, рассмотренного в Примере 7 п. 6.3.

Решение. Эрбрановский базис A = { P (a), Q (a), P(f (a)), Q(f(a)), P(f(f(a))),Q(f (f (a)))),... } имеет счётное число эле-ментов. Обозначая отрицание через ~, полное семантичес-кое дерево Т(S) можно представить в следующем виде:

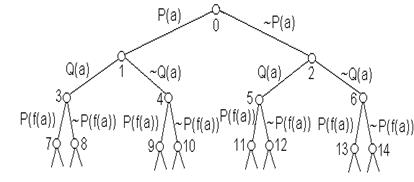
Рис.3.23

Для определенности все узлы в Т(S) пронумеруем сле-дующим образом: корню присваиваем номер 0, узлам пер-вого уровня (слева направо) - номера 1,2; узлам второго уровня (слева направо) - номера 3,4,5,6;...; узлам i -го уровня – номера 2ⁱ -1, 2ⁱ , 2ⁱ +1,..., 2ⁱ⁺¹ -2 и т.д.

Рассмотрим полное семантическое дерево Т(S), соот-ветствующее некоторой невыполнимой формуле В. Если S – множество дизъюнктов, соответствующее В, то это озна-чает, что каждая Н - интерпретация опровергает хотя бы один из его дизъюнктов D_i. Поскольку каждый дизъюнкт D_i содержит конечное число литер, то его опровержение должно произойти в некотором внутреннем узле полного семантического дерева Т(S).

Определение. Узел j полного семантического дерева Т(S) называется опровергающим, если все интерпретации I(j), содержащие его, опровергают некоторый основной при-мер дизъюнкта D_i Î S, а все узлы, лежащие выше j, не опро-вергают ни одного из D_i Î S.

Пример 2. Построить полное семантическое дерево Т(S) для множества дизъюнктов S = {Ø PÚ Q, Ø QÚ Ø R, ØPÚ R, P}, выявить опровергающие узлы в нем.

Решение. В данном случае матрица формулы является фор-мулой алгебры логики. Её эрбрановский универсум H(S) = Æ, A¢ = Æ, F¢ = Æ. Эрбрановский базис А={ P, Q, R }. Обозначая отрицание через ~, полное семантическое дере-во можно представить в виде:

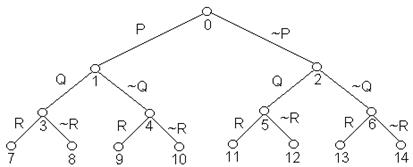
Рис.3.24

Для определённости будем считать, что атомы базиса P = И, Q=И, R=И, а их отрицания - ложны. Тогда

а) узел 2 будет опровергать дизъюнкт D₄ = P Î S,

б) узел 4 будет опровергать дизъюнкт D₁ =Ø PÚ Q Î S,

в) узел 7 будет опровергать дизъюнкт D₂ = Ø Q Ú Ø R Î S,

г) узел 8 будет опровергать дизъюнкт D₃ = Ø PÚ R Î S.

Если некоторый узел j полного семантического дере-ва Т(S) является опровергающим, то поддерево, выходящее из него, можно не рассматривать, поскольку все интерпре-тации, проходящие по этим узлам, будут опровергающими. Следовательно, его можно не показывать на схеме.

Определение. Семантическое дерево Т_з(S) называется закрытым, если каждая его ветвь заканчивается опровер-гающим узлом.

Семантическое дерево Т(S) в Примере 2 является за-крытым. Для таких деревьев применяют специальные изо-бражения, на которых опровергающие узлы перечёркивают и отбрасывают поддеревья, выходящие из них. Дерево Т_з(S) из Примера 2 примет при этом следующий вид:

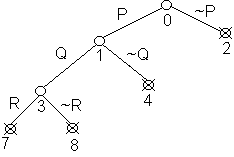
Рис.3.25

Теорема Эрбрана. Множество дизъюнктов S невы-полнимо Û когда любому полному семантическому дереву T(S) соответствует конечное закрытое семантическое дерево Т_з(S).

Существование закрытого семантического дерева Т_з(S) указывает на то, что любая Н - интерпретация приводит к появлению ложных дизъюнктов в S, что эквивалентно опровержимости S.

Алгоритм проверки невыполнимости формул при помощи семантического дерева.

1. Формула В представляется в виде пренексной нормаль-ной формы В¢ с матрицей М в виде конъюнкции дизъ-юнктов.

2. Путем устранения кванторов существования В¢ приво-дится к скулемовской форме, бескванторная часть которой рассматривается как множество дизъюнктов S.

3. Строится эрбрановский универсум H(S) и эрбрановский базис А.

4. Строится семантическое дерево по уровням. В каждом из них производится проверка узлов j на опровержимость (бу-дут ли интерпретации I(j) опровергать хотя бы один дизъ-юнкт D_i из S).

Если узел j является опровержимым, то узел отме-чается (обычно - зачеркиванием) и дальнейшее построение дерева из него прекращается.

Если узел j не является опровержимым, то построение дерева из него продолжается.

5. Если на некотором шаге дальнейшее построение дерева оказалось невозможным (поскольку все построенные кон-цевые узлы оказались опровержимыми), то множество дизъ-юнктов S, а, следовательно, и исходная формула В – невы-полнимы.

Если построение семантического дерева продолжает-ся, то на вопрос о невыполнимости S нельзя дать ни поло-жительный, ни отрицательный ответ.