2015-05-29
741
Нобелевский лауреат Роберт Солоу из Массачусетсского технологического института разработал модель факторного анализа источников экономического роста. Отправной точкой является производственная функция[1]. Представим выпуск (Q) в виде функции от основного капитала (К), вложенного труда (L) и уровня развития технологии (Т):
Q=Q(K,L,T). (1)
Солоу показал, как рост выпуска Q происходит при росте отдельных факторов, т.е. за счет роста К, L, Т. Чтобы получить такое уравнение, Солоу предположил, что производственная функция имеет особый вид, а именно: изменение Т приводит к одинаковому увеличению предельного продукта К и L. Это выполняется, если уравнение (1) записать в виде:
Q=TF(K, L), (2)
где F(K, L) — обычная неоклассическая производственная функция, зависящая от капитала и труда.
На основе уравнения (2) можно записать изменения в выпуске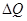 
следующим образом:
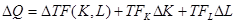. (3)
В уравнении (3) TFK — предельный продукт капитала, TFL — предельный продукт труда. Такая запись означает, что изменение выпуска 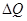пропорционально распределяется между 
, 
, 
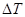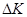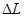. (К примеру, доля изменения L в изменении выпуска равна 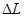, умноженному на предельный продукт труда TFL.)
Если использовать производственную функцию с постоянным эффектом масштаба и предположить, что экономика находится в условиях совершенной конкуренции, то TFl будет равно w/P, т.е. зарплате в единицах выпуска. Отсюда (TFlL)/Q равно доле издержек на рабочую силу в суммарном выпуске, которую мы обозначим sL. Аналогично (TFKK)/Q равно доле капитальных издержек в суммарном выпуске, которую мы обозначим как sK. Сумма долей труда и капитала равна единице, т.е. sL+sK = 1.
Сделав это, мы можем переписать уравнение (3) в следующем виде:
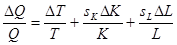. (4)
Эта запись означает, что темп роста выпуска (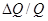
) равен сумме трех слагаемых: 1) темпа технического прогресса (
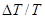); 2) темпа роста объема вложенного труда ( 
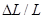), умноженного на зарплату в единицах выпуска sL; 3) темпа прироста капитала ( 
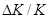), умноженного на коэффициент, равный доле капитала в выпуске (sK).
Используя уравнение (4), мы можем рассчитать величину роста выпуска на единицу вложенного труда, т.е. рост Q/L. Вспомнив, что относительное изменение величины дроби равно относительному изменению числителя минус относительное изменение знаменателя, получим, что увеличение Q/L в процентах равно 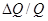— 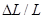. Затем, вычитая 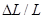из обеих частей уравнения (4), получаем:
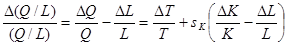. (5)
Если принять для простоты темп роста населения равным темпу роста рабочей силы, то выражение (5) покажет вклад в рост выпуска на душу населения двух факторов: темпа технического прогресса 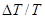и темпа роста капитала на одного работающего ( 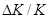- 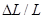), умноженного на коэффициент, равный доле капитала sK. (Заметьте, что 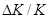- 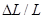также равняется ∆(K/L)/(K/L).)
Как правило, технический прогресс не может быть измерен непосредственно. Поэтому уравнение (5) обычно не может быть проверено эмпирически, хотя предполагается, что оно выполняется. Это уравнение используется для подсчета ∆ Т/Т как остаточного элемента после того, как вклад поддающихся измерению факторов экономического роста определен и вычтен из ∆(Q/L)/(Q/L). В частности, выражение (5) может быть переписано в следующем виде:
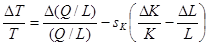(6)
Далее, ∆Т/Т можно рассчитать как разницу между наблюдаемым темпом роста выпуска на одного рабочего и изменением капиталовооруженности одного рабочего, умноженным на долю капитала в выпуске. Это так называемый остаток Солоу.
Экономисты интерпретируют остаток Солоу как долю экономического роста за счет технического прогресса. Но в действительности остаток Солоу рассчитывается как часть экономического роста, которая обусловлена факторами, не поддающимися непосредственным измерениям.
