2015-05-29
4947
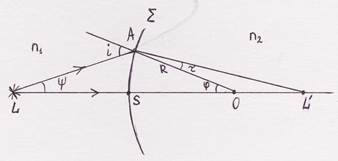
Рассмотрим узкий гомоцентрический конус лучей.
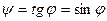– угол мал
, 
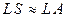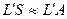– пучок параксиальный (приосевой) (1)
Будем считать расстояния, отсчитываемые от поверхности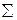 
влево – отрицательными, а от 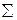вправо – положительными.
Из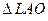 
по теореме синусов, получаем
,
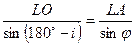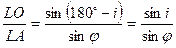. (2)
Из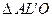 
следует
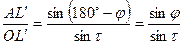. (3)
Уравнение (2) умножим на уравнение (3):
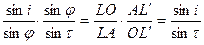, (4)
.
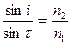Следовательно
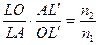. (5)
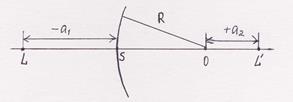
Введем следующие обозначения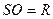 
, 
, 
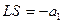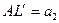(6)
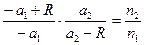(7)
,
,
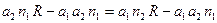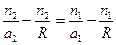следовательно
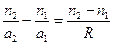. (8)
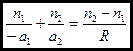(9)
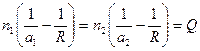, (10)
следовательно произведение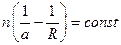 
и называется нулевым инвариантом Аббе.
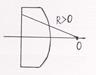
Пользуясь правилом знаков
а)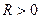 
– поверхность 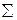выпуклая а) b)
(11)
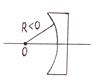
b)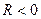 
– поверхность 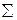вогнутая
Применим (9) для сферического зеркала:
, 
,
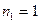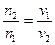так как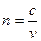 
или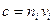 
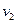после отражения равно 
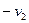(или 
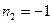), то
.
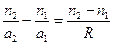Следовательно
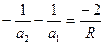(13)
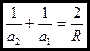(14)
Если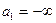 
, тогда 
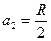от поверхности 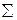. Это расстояние называется фокусным расстоянием.
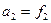
При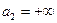 
, тогда
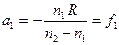. (18)
где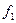 
и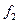 
зависят только от 
, 
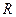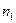и 
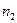. Следовательно, 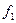и 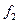для заданных 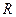, 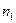и 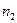являются постоянными.
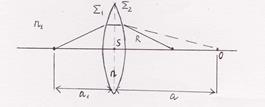Для тонкой линзы с 
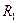и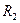 
Для поверхности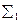 
:
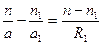(для левой) (19)
Для поверхности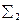 
:
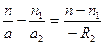(для правой) (20)
или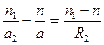 
.
|
|
|
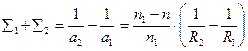
Обозначая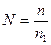 
, получаем
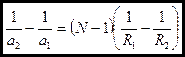(21)
Частные случаи:
1) Симметричная линза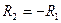 
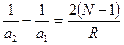и 
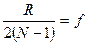(22)
.
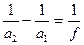2) Линза в воздухе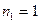
,
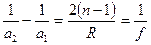следовательно
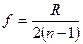(23)
Если лучи не близкие к оси системы, то погрешности превышают аберрации оптической системы.
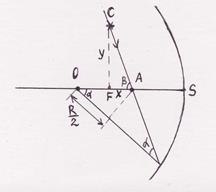
О – центр, F – фокус
, 
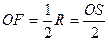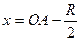
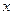– продольная аберрация, 
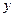– поперечная аберрация
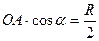, следовательно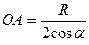 
, 
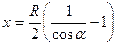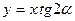(24)
так как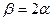 
.
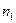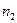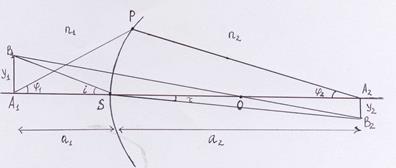
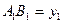Формирование изображения предмета, имеющего конечные размеры, сферической поверхностью раздела двух сред с показателями преломления и .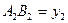
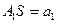и 
и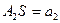 
,
,
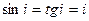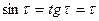
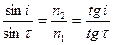следовательно
, 
.
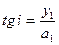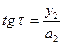Тогда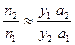 
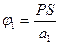и 
,
следовательно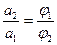 
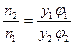или
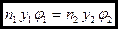– теорема Лагранжа-Гельгмгольца
Для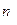 
сред
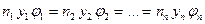(25)
Применительно к зеркалу, то есть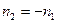 
из этой теоремы получаем
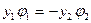
следовательно
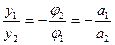. (26)
Если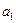 
и 
и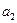меют одинаковые знаки, то есть изображение находится перед зеркалом, следовательно – действительное, то отношение 
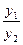– отрицательное; изображение перевернуто по отношению к предмету.
Если изображение мнимое, то есть 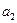– отрицательное, то 
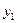и 
и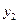меют одинаковые знаки; изображение – прямое.
