Подходы к решению проблемы гетероскедастичности

1-й общий подход к решению данной проблемы состоит в преобразовании исходных данных таким образом, чтобы для преобразованных данных модель уже обладала свойством гомоскедастичности. Применяют чаще всего два вида преобразований а) логарифмирование данных; б) переход к безразмерным величинам путем деления на некоторые известные величины, той же размерности, что и исходные данные. Возможна также стандартизация исходных данных.

Второй подход состоит в применении взвешенного и обобщенного метода наименьших квадратов.

Вычитая из данных X(ti) выровненные значения 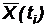, получаем остатки, случайную составляющую тренда

e(t) =X(t) - 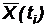. (5.14)

Обычно считается, что выравнивание удовлетворительное, если остатки e(t) образуют стационарный процесс с нулевым математическим ожиданием me(t) = M[e(t)] = 0.

Кроме того, для корректного применения МНК, необходимо более жесткое предположение, что e(t) – случайные независимые (хотя бы некоррелированные) величины с me(t) = 0. Если же e(ti) коррелируют между собой, то говорят, что в модели присутствует автокорреляция остатков. Метод наименьших квадратов и в этом случае дает несмещенные и состоятельные оценки коэффициентов уравнений кривых.

Однако, получаемые при этом стандартные ошибки и доверительные интервалы для коэффициентов оказываются заниженными.

Это может привести к ошибочным выводам при оценке качества отобранной модели поведения временного ряда. Значительная корреляция остатков сигнализирует о том, что, либо кривая 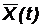подобрана неудачно, либо придется строить еще одну модель для описания поведения самих остатков e(ti).

Итак, при анализе модели тренда необходимо определить присутствует или нет автокорреляция в e(ti). Предварительную оценку случайности поведения остатков проводят на основе критерия поворотных точек. В соответствии с ним каждое значение e(ti) ряда остатков сравнивается с двумя рядом стоящими значениями e(ti – 1) и e(ti + 1).

Если e(ti) > e(ti– 1 ) и e(ti) > e(ti+ 1 ) или e(ti) < e(ti– 1 ), e(ti) < e(ti+ 1 ), то точка e(ti) считается поворотной (в ней достигается локальный максимум или минимум). Далее подсчитывается общее количество поворотных точек P. В случайном ряду остатков должно выполнятся строгое неравенство:

P > [2 (n – 2 )/ 3 – 2 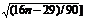. (5.15)

Квадратные скобки здесь означают, что берется целая часть числа (не путать с процедурой округления). Отметим, что критерий поворотных точек сигнализирует только о наличии положительной корреляции в ряде остатков. Если число поворотных точек P велико, приближается к n – 2, то можно говорить о наличии отрицательной корреляции между соседними членами временного ряда остатков. Критерий поворотных точек является предварительным и его следует дополнить другими, более точными критериями.