Если при 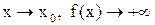 и
и 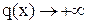 , то разность
, то разность 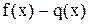 представляет собой неопределенность
представляет собой неопределенность 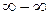 . Чтобы раскрыть такую неопределенность, надо привести её к виду
. Чтобы раскрыть такую неопределенность, надо привести её к виду 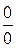 или
или 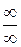 .
.
Вычислить предел 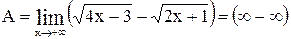 .
.
Умножим и разделим на сопряженное выражение 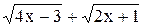 , тогда
, тогда
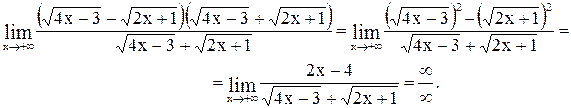
Здесь старшая степень 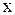 - первая, поэтому
- первая, поэтому
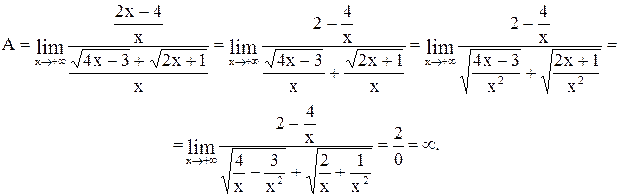
Две бесконечно малые функции 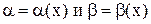 при
при 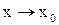 или
или 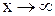 называются эквивалентными, если предел их отношения равен единице. Эквивалентность бесконечно малых функций записывается в виде
называются эквивалентными, если предел их отношения равен единице. Эквивалентность бесконечно малых функций записывается в виде 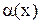 ~
~ 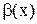 .
.
Таким образом, если 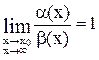 , то
, то 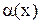 ~
~ 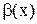 .
.
Таблица эквивалентных бесконечно малых функций
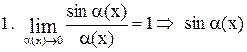 ~ ~ 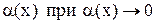 . .
|
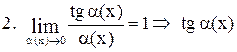 ~ ~ 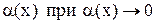 . .
|
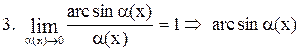 ~ ~ 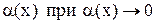
|
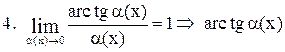 ~ ~ 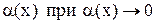 . .
|
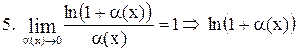 ~ ~ 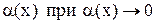 . .
|
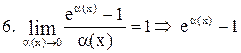 ~ ~ 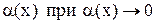 . .
|
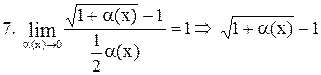 ~ ~ 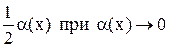 . .
|
Теорема. Предел отношения двух бесконечно малых не изменится, если одну или обе бесконечно малые заменить им эквивалентными, т. е. если 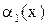 ~
~ 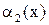 и
и 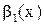 ~
~ 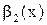 , то
, то 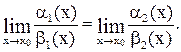
Заметим, что с помощью эквивалентных бесконечно малых раскрывают неопределенность 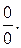
 2015-05-30
2015-05-30 279
279








