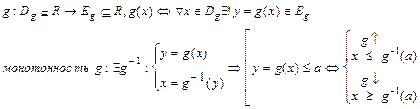
Пусть задана СВ Х и числовая функция 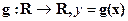 , определяющая на Х
, определяющая на Х
СВ Y=g(X).
(1) Если X - ДСВ {X={xi};PX={p(xi}},СВ Y=g(X) определена как событие на Х:
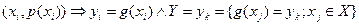 , является ДСВ и её математическая модель имеет вид:
, является ДСВ и её математическая модель имеет вид:
{{yk}; {P(yk)= 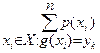 }}
}}
Пример. g(x)=x2
| X={Xi} | p(xi) | Y={yk} | p(yk) | (yk)2 |
| -3 | 0.1 | 0.2 | ||
| -2 | 0.2 | 0.4 | ||
| -1 | 0.1 | 0.2 | ||
| 0.2 | 0.2 | |||
| 0.1 | MY=3.6 | 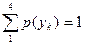
| MY2= 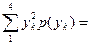 22.8
DY= 22.8
DY= 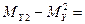 9.84
σY 9.84
σY 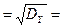 ≈ 3.137 ≈ 3.137
| |
| 0.2 | ||||
| 0.1 | ||||
| MX=0 | 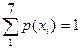
|
(2) Пусть НСВ X задана плотностью f(x) илифункцией распределения F(x)
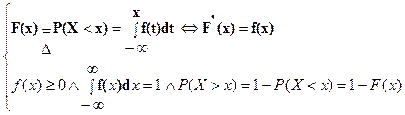 ,
,
и 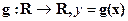 - строго монотонная числовая функция.
- строго монотонная числовая функция.
Требуется найти плотность fY(y) и функцию распределения FY(y) СВ Y=g(X).
По определению
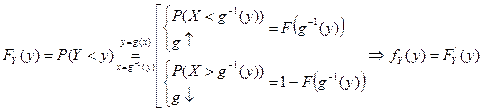
Пример Найти функцию FY (y), плотность fY (y) распределения и числовые характеристики
СВ Y= g(x)=e-Х, если
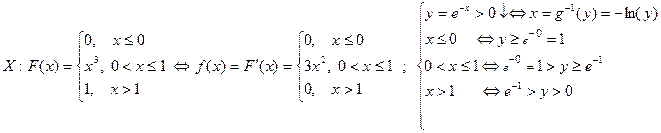
è 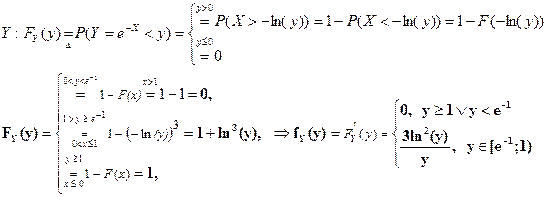
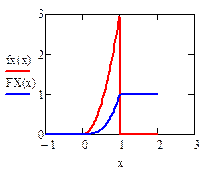
|
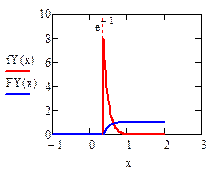
|
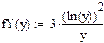
|
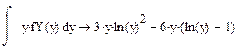
|
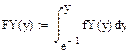
|
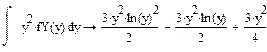
|
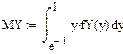
|
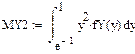
|
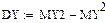
|
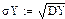
|
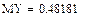
|
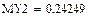
|
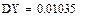
|
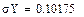
|
Утверждение 1
Если функция g имеет обратную g-1 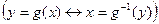 , то плотность распределения СВ Y=g(X) находится по формуле:
, то плотность распределения СВ Y=g(X) находится по формуле:
fY(y)=|(g-1(y))’|∙ fX(g-1(y)) (1)
Для 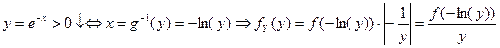
Утверждение 2
Если функция 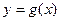 является кусочно монотонной – имеет обратные функции на интервалах монотонности
является кусочно монотонной – имеет обратные функции на интервалах монотонности 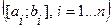 , плотность распределения СВ Y=g(X) находится по формуле:
, плотность распределения СВ Y=g(X) находится по формуле:
|
|
|
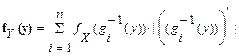 (2)
(2)
è Функция y=g(x)=x2 имеет две обратные: 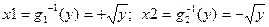 . Плотность распределения СВ Y=g(X)=X2 находится по формуле:
. Плотность распределения СВ Y=g(X)=X2 находится по формуле:
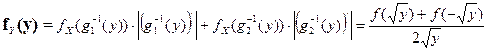
=============================================
ИДЗ-4 «Функции случайной величины»
Задание. Используя результаты ИДЗ-3 для НСВ Х, найти плотность, функцию распределения и вычислить числовые характеристики СВ Y=e-X.
 2015-05-30
2015-05-30 241
241






