2015-05-30
2064
Интервальный ряд с интервалами, возрастающими в геометрической прогрессии: ширина каждого последующего интервала ii+1 больше предыдущего ii в определенное число раз g (знаменатель геометрической прогрессии).
ii+1 = ii *g
В этом случае размах вариации
R = верхняя граница последнего интервала – нижняя граница первого интервала
будет равен сумме первых n членов геометрической прогрессии
R=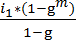 
,
R=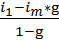 
где m – количество интервалов, g – знаменатель прогрессии,
i1 – ширина первого интервала, im – ширина последнего интервала.
Используя эти формулы, можно определить ширину первого интервала и знаменатель прогрессии.
Интервальный ряд с интервалами, убывающими в геометрической прогрессии: ширина каждого последующего интервала ii+1 меньше предыдущего ii в определенное число раз g (знаменатель геометрической прогрессии).
ii+1 = ii /g
В этом случае размах вариации
R = верхняя граница последнего интервала – нижняя граница первого интервала
будет равен сумме первых n членов геометрической прогрессии
|
|
|
R=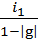 
,
Используя эти формулы, можно определить ширину первого интервала и знаменатель прогрессии.
Внимание!
Полигон распределения частот, гистограмма строятся также с использованием абсолютной плотности распределения вместо частоты и относительной плотности распределения вместо частости.
Абсолютная плотность распределения (р) представляет собой величину частоты, приходящейся на единицу размера интервала отдельной группы ряда:
р = f / i.
Мода для интервального вариационного ряда с неравными интервалами осуществляется по уже известной формуле, только вместо показателей частот f используются показатели плотности распределения p, которые обеспечивают сопоставимость неравных интервалов.
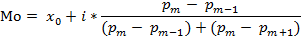
где:
1. 
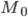— значение моды
2. 
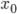— нижняя граница модального интервала
3. i —ширина интервала (верхняя граница интервала – нижняя граница)
4. pm — абсолютная плотность распределения модального интервала
5. pm-1 — абсолютная плотность распределения интервала, предшествующего модальному
6. pm+1 — абсолютная плотность распределения интервала, следующего за модальным
ПРИМЕР
Рассмотрим пример построения ряда с неравными интервалами.
Исходные данные приведены в таблице
| Название компании | объем реализации, млн.руб. |
| Микротест | 5,7 |
| Открытые технологии | 6,9 |
| КРОК | |
| НТ Компьютер | 9,7 |
| Верисел | 11,6 |
| Техносервис | 15,2 |
| IBS | 16,3 |
| Ланит | 17,2 |
| НКК | 22,7 |
| Ситроникс |
Для построения интервального ряда с равными интервалами рассчитаем:
| эффективное число групп | 4,322 |
| округляем эффективное число групп до целого большего | |
| максимальное значение | |
| минимальное значение | 5,7 |
| .i (ширина интервала) | 4,26 |
Если взять ширину интервала 4, то получится следующий ряд:
|
|
|
| номер интервала | нижняя граница | верхняя граница |
Полученные интервалы не включают в себя все значения. Следовательно, берем ширину интервала, равную 5.
Получаем интервальный ряд:
| номер интервала | нижняя граница | верхняя граница | частоты |
| ИТОГО |
Строим полигон распределения частот и гистограмму распределения частот:
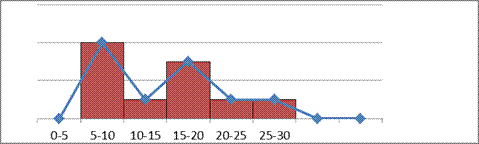
Видно, что распределение компаний по интервалам неравномерное, линия полигона распределения частот зигзагообразная, имеются малочисленные интервалы.
Поэтому построим несколько вариантов ряда с неравными интервалами и выберем лучший.
1) Построим равночастотный квинтильный интервальный ряд:
| нижняя граница | верхняя граница | частоты | ширина интервала | Абсолютная плотность распределения |
| (1) | (2) | (3) | (2-1)=(4) | (5)=(3/4) |
| 1,000 | ||||
| 0,667 | ||||
| 0,333 | ||||
| 1,000 | ||||
| 0,222 |
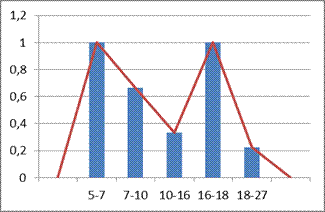
Проблема не решена – зигзаги сохраняются
2) Строим ряд с произвольными интервалами, в которых коэффициент вариации не превышает 20%.
| интервал | частота | V |
| 0-8 | 0,189419 | |
| 8-16 | 0,187466 | |
| 16-24 | 0,151005 | |
| 24-32 | ||
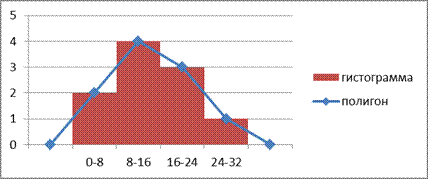
3) Строим ряд с интервалами, возрастающими в арифметической прогрессии
ii+1 = ii + a
ширина первого интервала – 3, а=1,
| номер интервала | нижняя граница | верхняя граница | ширина интервала | частота | абсолютная плотность распределения |
| (1) | (2) | (3)=(2+4) | (4) | (5) | (6)=(5/4) |
| 0,250 | |||||
| 4=3+1 | 0,250 | ||||
| 5=4+1 | 0,118 | ||||
| 6=5+1 | 0,087 | ||||
| 7=6+1 | 0,033 |
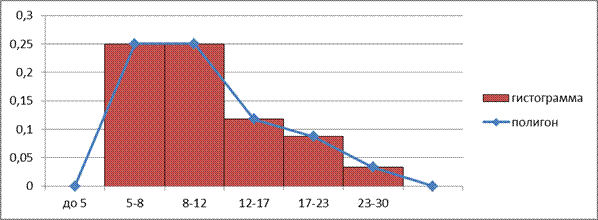
4) Построим ряд с интервалами, убывающими в арифметической прогрессии
ii+1 = ii - a
| номер интервала | нижняя граница | верхняя граница | ширина интервала | частота | абсолютная плотность распределения |
| (1) | (2) | (3)=(2+4) | (4) | (5) | (6)=(5/4) |
| 0,417 | |||||
| 0,167 | |||||
| 0,043 | |||||
| 0,037 | |||||
| 0,000 |
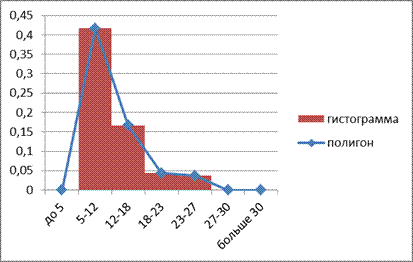
5) Построим ряд с интервалами, возрастающими в геометрической прогрессии
ii+1 = ii * a
| номер интервала | нижняя граница | верхняя граница | ширина интервала | частота | абсолютная плотность распределения |
| (1) | (2) | (3)=(2+4) | (4) | (5) | (6)=(5/4) |
| 0,286 | |||||
| 0,182 | |||||
| 0,211 | |||||
| 0,057 |
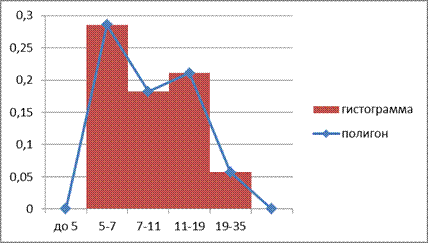
6) Построим ряд с интервалами, убывающими в геометрической прогрессии
ii+1 = ii / a
| номер интервала | нижняя граница | верхняя граница | ширина интервала | частота | абсолютная плотность распределения |
| (1) | (2) | (3)=(2+4) | (4) | (5) | (6)=(5/4) |
| 0,381 | |||||
| 0,069 | |||||
| 0,000 | |||||
| 0,000 |
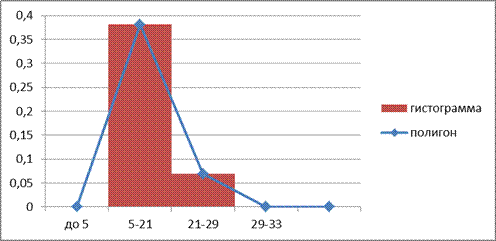
Итак, наиболее плавная линия полигона распределения частот, получается при построении ряда с интервалами, возрастающими в арифметической прогрессии, и в ряде с произвольными интервалами (у нас получились равные). Эти ряды и нужно использовать для дальнейших расчетов.
Но какой именно? На этот вопрос поможет ответить эмпирическое корреляционное отношение. Нужно использовать ряд с максимальным эмпирическим корреляционным отношением.
а) Рассчитаем эмпирическое корреляционное отношение для ряда с произвольными интервалами
| группа | Компания | объем реализации, млн.руб. | дисперсия по группе | частота группы | |
| (1) | (2) | (3) | (4) | (5) | (4*5) |
| 0-8 | Микротест | 5,7 | 0,3600 | 0,7200 | |
| Открытые технологии | 6,9 | ||||
| 8-16 | КРОК | 5,7819 | 23,1275 | ||
| НТ Компьютер | 9,7 | ||||
| Верисел | 11,6 | ||||
| Техносервис | 15,2 | ||||
| 16-32 | IBS | 16,3 | 8,0022 | 24,0067 | |
| Ланит | 17,2 | ||||
| НКК | 22,7 | ||||
| Ситроникс | 0,0000 | 0,0000 | |||
| Итого | 47,8542 | ||||
| общая дисперсия | 43,0041 | ||||
| случайная дисперсия | 4,7854 | ||||
| факторная дисперсия | 38,2187 | ||||
| эмпирическое корреляционное отношение | 0,9427 |
б) Рассчитаем эмпирическое корреляционное отношение для ряда с неравными интервалами
|
|
|
| группа | Компания | объем реализации, млн.руб. | дисперсия по группе | частота группы | |
| (1) | (2) | (3) | (4) | (5) | (4*5) |
| 5-8 | Микротест | 5,7 | 0,3600 | 0,7200 | |
| Открытые технологии | 6,9 | ||||
| 8-12 | КРОК | 1,2067 | 3,6200 | ||
| НТ Компьютер | 9,7 | ||||
| Верисел | 11,6 | ||||
| 12-17 | Техносервис | 15,2 | |||
| IBS | 16,3 | 0,3025 | 0,6050 | ||
| 17-23 | Ланит | 17,2 | |||
| НКК | 22,7 | 7,5625 | 15,1250 | ||
| 23-30 | Ситроникс | 0,0000 | 0,0000 | ||
| Итого | 20,0700 | ||||
| общая дисперсия | 43,0041 | ||||
| случайная дисперсия | 2,0070 | ||||
| факторная дисперсия | 40,9971 | ||||
| эмпирическое корреляционное отношение | 0,9764 |
Для ряда с неравными интервалами эмпирическое корреляционное отношение больше, следовательно, это – самый удачный вариант группировки наших данных.
