Полосы равной толщины. Кольца Ньютона

Пусть на пластинку в виде клина с углом при вершине 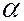падает плоская волна, направление распространения которой совпадает с параллельными лучами 1 и 2. Лучи 1¢ и 1¢¢ отразившиеся от верхней и нижней грани после прохождения через линзу пересекутся в некоторой точке А, являющейся изображением точки В. Так как эти лучи когерентны, они будут интерферировать. При небольшом угле 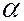разность хода лучей 1¢ и 1¢¢ можно с достаточной степенью точности вычислять по формуле (6.36.13), где 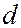– толщина клина в месте падения. Лучи 2' и 2'', обрзовавшиеся за счет отражения луча 2, упавшего в точку, где толщина клина 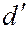, соберутся линзой в точке А'. Разность хода этих лучей определяется толщиной .

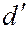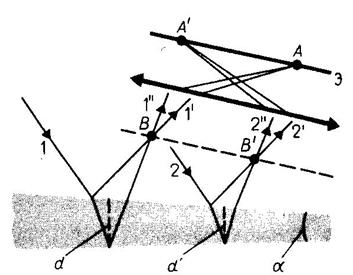На экране возникает система светлых и темных интерференционных полос. Каждая из полос возникает при отражении от мест пластинки, имеющих одинаковую толщину. Такие полосы называются полосами равной толщины. Полосы равной толщины локализованы вблизи пластинки – в точках В и В'.

При наблюдении в белом свете полосы будут окрашены (расплывшиеся на поверхности воды тонкие пленки нефти или масла, мыльные пленки, цвета побежалости на поверхности стальных изделий после закалки).

Кольца Ньютона являются классическим примером полос равной толщины, наблюдаются при отражении света от воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны 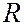. Параллельный монохроматический пучок света с длиной волны 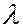падает нормально на плоскую поверхность линзы с коэффициентом преломления 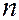и частично отражается от верхней и нижней поверхностей воздушного зазора. При наложении отраженных лучей образуются полосы равной толщины, имеющие вид концентрических светлых и темных колец. Если толщина воздушного зазора в месте отражения равна 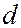, то оптическая разность хода лучей, отразившихся от верхней и нижней поверхностей воздушного зазора (с учетом потери половины волны при отражении от стеклянной пластинки) равна

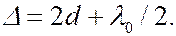(6.36.16)

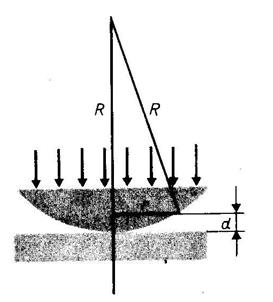Толщина воздушного зазора 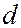связана с радиусом окружности 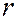, на которой расположены точки с одинаковым зазором, соотношением

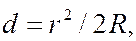(6.36.17)

где 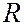– радиус кривизны поверхности линзы. Отсюда,

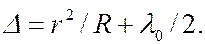(6.36.18)

Приравнивая (6.36.18) к условиям максимума и минимума интерференции, получаем:

радиус 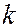-го светлого кольца равен:

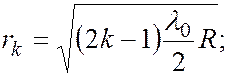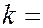( 1, 2, 3,) (6.36.19)

радиус 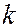-го темного кольца равен:

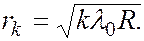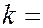( 0, 1, 2, 3 …..) (6.36.20)

При наблюдении в белом свете полосы получаются окрашенными.