Представим себе потребителя, который решает, сколько данного товара потребить в каждом из двух временных периодов. Мы, как правило, будем считать такой товар композитным товаром, подобным описанному в главе 2, но можно, если хотите, считать его и конкретным товаром. Обозначим величину потребления в каждом периоде через (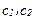 ) и предположим, что цены потребления в каждом периоде постоянны и равны 1. Сумму денег, имеющуюся у потребителя в каждом периоде, обозначим через (
) и предположим, что цены потребления в каждом периоде постоянны и равны 1. Сумму денег, имеющуюся у потребителя в каждом периоде, обозначим через (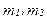 ).
).
Вначале предположим, что единственный способ, которым потребитель может перевести деньги из периода 1 в период 2, - это сбережение денег без получения процента. Более того, пока предположим, что у него нет возможности занимать деньги, так что максимальная сумма, которую он может истратить в периоде 1, есть 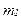 . Тогда его бюджетное ограничение будет иметь такой же вид, как на рис.10.1.
. Тогда его бюджетное ограничение будет иметь такой же вид, как на рис.10.1.

Рис.10.1 Бюджетное ограничение. Это - бюджетное ограничение для случая, когда ставка процента равна нулю и брать деньги взаймы не разрешается. Чем меньше потребит данный индивид в период 1, тем больше он может потребить в период 2.
Мы видим, что у потребителя имеется выбор двоякого рода. Он может предпочесть потреблять в точке (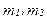 ), что означает просто потребление своего дохода в каждом периоде, или же может предпочесть потребить в периоде 1 не весь свой доход. В этом последнем случае потребитель откладывает часть потребления первого периода на более позднее время.
), что означает просто потребление своего дохода в каждом периоде, или же может предпочесть потребить в периоде 1 не весь свой доход. В этом последнем случае потребитель откладывает часть потребления первого периода на более позднее время.
Теперь позволим потребителю брать и давать взаймы по некой ставке процента r. Сохраняя для удобства цены потребления в каждом периоде на уровне 1, выведем уравнение бюджетного ограничения. Сперва допустим, что потребитель решает делать сбережения, так что величина его потребления в первом периоде, 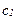 , меньше дохода первого периода,
, меньше дохода первого периода, 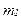 . В этом случае он заработает процент на сберегаемую им сумму,
. В этом случае он заработает процент на сберегаемую им сумму, 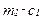 , исходя из ставки процента r. Сумма, которую он может израсходовать на потребление в следующем периоде, задана выражением
, исходя из ставки процента r. Сумма, которую он может израсходовать на потребление в следующем периоде, задана выражением
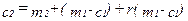
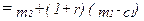 (10.1)
(10.1)
Оно говорит нам, что в периоде 2 потребитель может истратить на потребление сумму, равную его доходу плюс сумма сбережений, сделанных в период 1, плюс процент, заработанный на эти сбережения.
Предположим теперь, что потребитель является заемщиком, так что его потребление в первом периоде превышает его доход первого периода. Потребитель выступаетт заемщиком, если 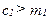 , и процент, который ему придется платить во втором периоде, составит
, и процент, который ему придется платить во втором периоде, составит 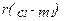 . Разумеется, ему придется также вернуть и взятую взаймы сумму,
. Разумеется, ему придется также вернуть и взятую взаймы сумму, 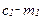 . Это означает, что его бюджетное ограничение задано уравнением
. Это означает, что его бюджетное ограничение задано уравнением
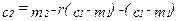
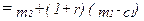 ,
,
что в точности совпадает с уравнением, записанным нами ранее. Если величина 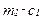 положительна, то потребитель зарабатывает процент на эти сбережения; если же величина
положительна, то потребитель зарабатывает процент на эти сбережения; если же величина 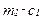 отрицательна, потребитель платит процент на взятую взаймы сумму.
отрицательна, потребитель платит процент на взятую взаймы сумму.
Если 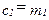 , то с необходимостью и
, то с необходимостью и 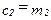 , и потребитель не является ни заемщиком, ни кредитором. Мы можем назвать эту потребительскую позицию "точкой Полония".[8]
, и потребитель не является ни заемщиком, ни кредитором. Мы можем назвать эту потребительскую позицию "точкой Полония".[8]
Можно преобразовать уравнение бюджетного ограничения для данного потребителя, получив два полезных альтернативных вида этого уравнения:
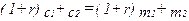 (10.2) (10.2)
|
и
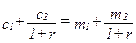 (10.3) (10.3)
|
Обратите внимание на то, что оба уравнения имеют форму
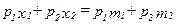 .
.
В уравнении (10.2) 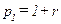 и
и 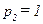 . В уравнении (10.3)
. В уравнении (10.3) 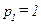 и
и 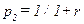 .
.
Мы говорим, что уравнение (10.2) выражает бюджетное ограничение через будущую стоимость, а уравнение (10.3) выражает бюджетное ограничение через текущую стоимость. Выбор данной терминологии объясняется тем, что в первом бюджетном ограничении цена будущего потребления равна 1, в то время как во втором бюджетном ограничении цена текущего потребления равна 1. В первом уравнении бюджетного ограничения цена потребления первого периода измерена относительно цены потребления второго периода, а во втором уравнении - наоборот.
Геометрическая интерпретация текущей и будущей стоимости дана на рис.10.2. Текущая стоимость начального запаса денег в двух периодах есть сумма денег в периоде 1, которая породила бы то же самое бюджетное множество, что и начальный запас денег. Эта сумма, показанная просто точкой пересечения бюджетной линии с горизонтальной осью, дает максимально возможную в первом периоде величину потребления. Как показывает бюджетное ограничение, эта сумма есть 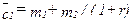 , что составляет текущую стоимость начального запаса.
, что составляет текущую стоимость начального запаса.
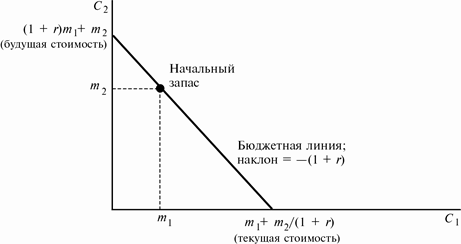
Рис.10.2 Текущая и будущая стоимости. Точка пересечения бюджетной линии с вертикальной осью показывает будущую стоимость, а точка ее пересечения с горизонтальной осью - текущую стоимость.
Аналогичным образом, точка пересечения бюджетной линии с вертикальной осью показывает максимальную сумму, расходуемую на потребление во втором периоде, которая соответствует 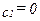 . И опять из уравнения бюджетного ограничения мы можем найти эту величину
. И опять из уравнения бюджетного ограничения мы можем найти эту величину 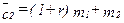 , представляющую собой будущую стоимость начального запаса.
, представляющую собой будущую стоимость начального запаса.
Выражение межвременного бюджетного ограничения через текущую стоимость имеет большее значение, поскольку с его помощью измеряется текущая стоимость будущего дохода, что соответствует обычному взгляду на эти сопоставления.
Любое из этих уравнений показывает нам вид данного бюджетного ограничения. Бюджетная линия проходит через точку (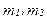 ), поскольку эта структура потребления всегда является доступной, и имеет наклон -(1+r).
), поскольку эта структура потребления всегда является доступной, и имеет наклон -(1+r).
 2015-05-30
2015-05-30 746
746








