(задачи с двумя звездочками)
1. (задача о рассеянной секретарше; см. задачу 18.220). Помимо общей формулы для 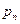 дать оценку остаточного члена.
дать оценку остаточного члена.
2. Колода в 36 карт наудачу разделяется на две равные части. Найти вероятность того, что в обеих частях окажется одинаковое количество карт красной и черной масти.
3. (преферансный расклад: «третья дама у вистующего»). Колода в 32 карты наудачу раздается на троих плюс 2 карты в прикуп. Прикуп уже взят – игрок определился, но игра еще не назначена. У игрока пять старших червей без дамы плюс пять карт других мастей. Игрок размышляет, какую игру ему назначить, ибо есть риск, что оставшиеся три карты червовой масти (третья дама) окажутся на руках у одного из вистующих. Найти вероятность указанного события.
4. (некоторые покерные расклады). Из колоды в 52 карты (джокеры для простоты отсутствуют) наудачу извлекают 5 карт. Найти вероятности следующих событий: A= {получена комбинация «стрит»}={5 последовательных по значению карт произвольных мастей}; B= {получена комбинация «каре»}={4 карты одинакового значения}; C= {получена комбинация «флешь ройяль»}={5 последовательных по значению карт одной масти}.
5. (из игры в бридж). 52 карты наудачу раздаются четверым игрокам. Найти вероятность 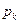 того, что у первого и второго игрока вместе окажутся ровно k тузов.
того, что у первого и второго игрока вместе окажутся ровно k тузов.
6. (задача о разделе ставки). Двое равносильных игроков играют матч до 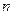 побед в игру без ничьих. Игра прервана при счете
побед в игру без ничьих. Игра прервана при счете 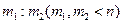 . Как следует справедливо разделить ставку между ними? В задаче 18.206 (1) рассматривается частный случай, предложенный итальянцем Паччоли в 1494г. для
. Как следует справедливо разделить ставку между ними? В задаче 18.206 (1) рассматривается частный случай, предложенный итальянцем Паччоли в 1494г. для 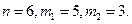 С тех пор ее очень долго решали. Правильный ответ получили независимо Б.Паскаль и П.Ферма только в 1654 г.
С тех пор ее очень долго решали. Правильный ответ получили независимо Б.Паскаль и П.Ферма только в 1654 г.
7. (парадокс Бертрана в классической постановке; см задачу 18.159 (1)).
8. (парадокс Бертрана в дискретной постановке).
9. (задача об оптимальном числе мест в кафе). 10 служащих одной фирмы каждый день обедают в одном из двух кафе, каждый раз выбирая его наудачу. Какое наименьшее число мест должно иметь каждое кафе, чтобы обслужить указанных служащих с надежностью 95%?
10. В единичный квадрат с вписанной в него окружностью наудачу бросаются 6 частиц. Найти вероятность того, что ни одна из полученных пяти областей квадрата не будет свободна от частиц.
11. n шаров наудачу рассыпаются по n ящикам (в каждый ящик входит любое число шаров, и все возможные распределения шаров по ящикам считаются равновероятными). Какова вероятность, что ровно один ящик останется пустым?
12. Из множества всех подмножеств множества 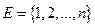 по схеме выбора с возвращением выбирается наудачу 2 подмножества
по схеме выбора с возвращением выбирается наудачу 2 подмножества 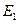 и
и 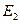 . Найти вероятность того, что они не пересекаются.
. Найти вероятность того, что они не пересекаются.
13. Имеется матрица 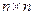 из случайных величин
из случайных величин 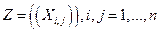 , причем случайные величины
, причем случайные величины 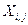 независимы в совокупности, центрированы и имеют одну и туже дисперсию
независимы в совокупности, центрированы и имеют одну и туже дисперсию 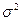 . Вычислить
. Вычислить 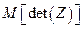 и
и 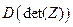 .
.
14. Случайные величины 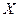 и
и 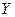 распределены каждая равномерно
распределены каждая равномерно 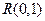 , но не являются независимыми. Доказать, что
, но не являются независимыми. Доказать, что 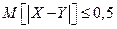 .
.
15. Случайные величины 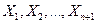 независимые индикаторные величины, т.е.
независимые индикаторные величины, т.е. 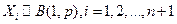 . Положим
. Положим 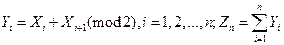 .
.
1) Найти 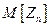 и
и 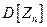 .
.
2) Доказать, что 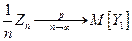 .
.
16. Случайный вектор 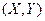 имеет нормальное распределение с характеристиками
имеет нормальное распределение с характеристиками 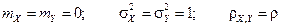 . Обозначим
. Обозначим 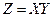 . Вычислить
. Вычислить 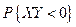 .
.
17. 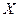 и
и 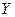 независимы и распределены каждая по закону Гео(p). Вычислить условную вероятность
независимы и распределены каждая по закону Гео(p). Вычислить условную вероятность 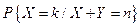 .
.
18. Случайные величины 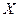 и
и 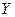 независимы и подчиняются одному распределению
независимы и подчиняются одному распределению 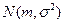 . Показать, что
. Показать, что 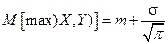 ,
, 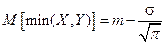 .
.
19. В жюри, состоящем из нечетного числа судей, каждый судья независимо от остальных принимает правильное решение с вероятностью 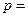 0,7. Каково должно быть наименьшее число членов жюри, при котором решение, принимаемое большинством голосов, будет правильным с гарантированной вероятностью 0,99?
0,7. Каково должно быть наименьшее число членов жюри, при котором решение, принимаемое большинством голосов, будет правильным с гарантированной вероятностью 0,99?
20. Пусть 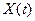 - пуассоновский процесс с параметром
- пуассоновский процесс с параметром 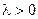 . Обозначим
. Обозначим 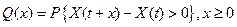 . Показать, что
. Показать, что 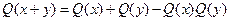 .
.
 2015-05-30
2015-05-30 1186
1186






