2015-05-22
2309
При сравнении смещенной оценки с несмещенной или двух оценок с разными величинами смещения полезным критерием служит средний квадрат ошибки (СКО) оценки, здесь ошибка измеряется относительно оцениваемого параметра для совокупности. Формально
CKO(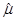
) = 
= 
=
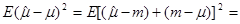
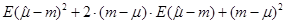= (дисперсия 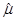)+ (смещение)2
(члены удвоенного произведения исчезают, так как Е(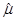 — т) = 0).
Применение СКО в качестве критерия достоверности оценки равносильно рассмотрению двух оценок, имеющих одинаковый СКО, как эквивалентных. Это не вполне строгое заключение, потому что распределения частот ошибок ( —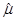 
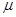) разной величины для двух оценок не будут одинаковы, если у них разные величины смещения. Однако, как показали Хансен, Хервиц и Мэдоу (Hansen, Hurwitz and Madow, 1953), если В/ 
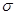меньше чем приблизительно 1/2, то распределения частот абсолютных величин ошибок 
почти одинаковы. Табл. 1.2 иллюстрирует это утверждение.
Даже при В/ 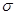= 0,6 соответствующие вероятности меняются незначительно по сравнению со случаем В/ 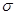= 0.
Поскольку трудно проследить за тем, чтобы в оценках не присутствовало никаких незаподозренных смещений, мы будем говорить обычно о точности (precision) оценки, а не о ее достоверности (accuracy). Термин достоверность относится к величине отклонений от истинного среднего значения 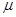, в то время как термин точность относится к величине отклонений от среднего значения т, получаемого в результате многократного применения одного и того же способа отбора. [[30]]
Таблица 1.2
ВЕРОЯТНОСТЬ ТОГО, ЧТО АБСОЛЮТНАЯ ВЕЛИЧИНА ОШИБКИ БОЛЬШЕ ИЛИ РАВНА:
1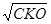 
; 1,96 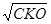; 2,576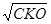
| B/s | Вероятость | ||
| 1 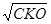| 1,96 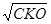| 2,576 | |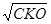
| 0,317 | 0,0500 | 0,0100 | |
| 0,2 | 0,317 | 0,0499 | 0,0100 |
| 0,4 | 0,319 | 0,0495 | 0,0095 |
| 0,6 | 0,324 | 0,0479 | 0,0083 |
[[31]]
* Данные относятся к началу 60-х годов.— Примеч. ред.
*Фамилия и год издания в скобках указывают на источник в списке литературы, помещенном в конце главы..— Примеч. ред.
* Далее слово «значение» будет иногда опускаться. – Примеч. ред.
** Английский термин standard error, который здесь употребляет автор, перелается термином стандартная ошибка, чтобы подчеркнуть терминологически отличие среднего квадратичного отклонения выборочной оценки (средней квадратичной ошибки) от среднего квадратичного отклонения вообще. – Примеч. ред.
