Абсолютная величина, характеризующая уровень признака отдельной единицы совокупности, не позволяет сравнивать значения признака у единиц, относящихся к разным совокупностям. Сравнивать можно лишь средние показатели.
Средняя величина – это обобщающий показатель, характеризующий типичный уровень явления. В средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами.
Средняя величина показывает уровень признака, отнесенный к единице совокупности, например, средняя заработная плата работников предприятия.
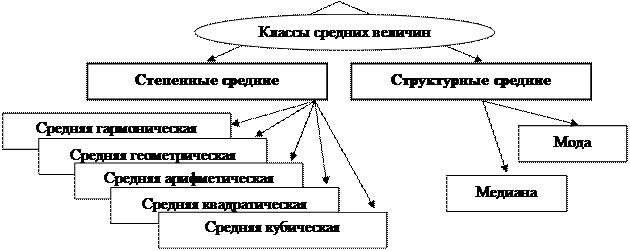
Классификация средних величин представлена на рис. 4.2.
Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными.
Простая средняя считается по несгруппированным данным и имеет общий вид:
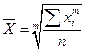 ,
,
где хi – варианта (значение) осредняемого признака; m – показатель степени средней; n – число вариант.
Взвешенная средняя считается по сгруппированным данным и имеет общий вид:
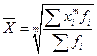 ,
,
где хi – варианта (значение) осредняемого признака или серединное значение интервала, в котором
Таблица 4.1
Типизация относительных величин
| Наименование относительных величин | Сущностная характеристика относительных величин | Методика расчета и название показателей |
| Относительная величина динамики | Характеризует изменение уровня развития какого-либо явления во времени | Получается в результате деления уровня показателя в определенный период или момент времени на уровень этого же показателя в предшествующий период или момент, и называется коэффициентом (индексом) роста(kр (iр)). Коэффициент роста, выраженный в процентах, называется темпом роста (Тр). Тр = kр х 100 Разность между величиной темпа роста и 100 % называется темпом прироста (Тпр). Тпр =Тпр - 100 |
| Относительная величина планового задания | Характеризует изменение планового уровня показателя на предстоящий период по сравнению с фактически сложившимся в предыдущем периоде | Рассчитывается как отношение уровня, запланированного на предстоящий период, к уровню, фактически сложившемуся в предыдущем периоде, называется коэффициентом (индексом) планового роста(kпл.з (iпл.з)).Коэффициент планового роста, выраженный в процентах, называется плановым темпом роста(Тр.пл.з), а разность между величиной планового темпа роста и 100 % - плановым темпом прироста (Тпр.пл.з) |
| Относительная величина выполнения задания | Характеризует степень выполнения задания | Рассчитывается как отношение фактически достигнутого в данном периоде уровня к запланированному, и называется коэффициентом (индексом) выполнения задания (плана) (kвып.пл.з (iвып.пл.з)), который в процентном выражении называется процентом выполнения задания, а разность между его величиной и 100% - процентом перевыполнения задания (плана) |
| Относительная величина структуры | Характеризует долю составного элемента в общем итоге. Их совокупность показывает строение изучаемого явления | Рассчитывается как отношение уровня части совокупности к суммарному уровню совокупности, называется долей или удельным весом, и, как правило, представляется в форме процентного содержания (d). |
| Относительная величина координации | Показывает, во сколько раз одна часть совокупности больше другой или сколько единиц одной части приходится на 1, 10 и т.д. единиц другой части | Рассчитывается как отношение частей данной совокупности к одной из них, принятой за базу сравнения |
| Относительная величина сравнения | Характеризует сравнительные размеры одноименных абсолютных величин относящихся к различным объектам или территориям | Рассчитывается как отношение одноименных абсолютных величин, относящихся к одному и тому же периоду или моменту времени, но к различным объектам или территориям |
| Относительная величина интенсивности | Отражает степень рас-пределения или развития явления в той или иной среде | Получают сопоставлением разноименных величин (показателей), относящихся к одному и тому же явлению и одинаковому периоду или моменту времени |
 |
|
Рис.4.2. Виды средних величин
изменяется варианта; m – показатель степени средней; fi – частота (вес), показывающая, сколько раз встречается i -е значение осредняемого признака.
Веса в формулах средних показывают повторяемость данного значения признака.
Методика расчета степенных средних приведена в табл. 4.2.
Таблица 4.2
Виды степенных средних и методика их расчета
| Вид степенной средней | Показатель степени (m) | Формула расчета | |
| простой средней | Взвешенной средней | ||
| Гармоническая | - 1 | 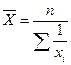
| 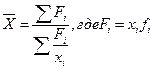
|
| Геометрическая | 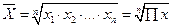
| 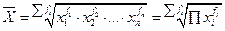
| |
| Арифметическая | 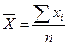
| 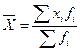
| |
| Квадратическая | 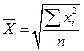
| 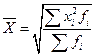
| |
| Кубическая | 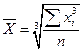
| 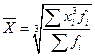
|
Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени m увеличивается и соответствующая средняя величина:
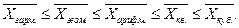
Виды средних величин различаются, прежде всего, тем, какое свойство, какой параметр исходной варьирующей массы индивидуальных значений признака должен быть сохранен неизменным. Необходимо, чтобы все этапы расчета средней величины имели реальное содержательное обоснование.
К средней гармонической простой следует прибегать в случаях определения, например, средних затрат труда, времени, материалов на единицу продукции, на одну деталь по двум (трем, четырем и т.д.) предприятиям, рабочим, занятым изготовлением одного и того же вида продукции, одной и той же детали, изделия.
Формула средней геометрической используется, чаще всего, при расчете среднего значения по индивидуальным относительным величинам динамики, например, темпам роста. Кроме того, геометрическая средняя величина дает наиболее правильный по содержанию результат осреднения, если задача состоит в нахождении такого значения признака, который качественно был бы равно удален как от максимального, так и от минимального значения признака.
Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным. Иначе можно сказать, что средняя арифметическая величина – среднее слагаемое.
Средней средних арифметических величин является средняя хронологическая. Она используется в том случае, если уровни, по которым нужно исчислить среднюю величину, заданы на определенный момент (период) времени:
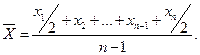
Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то средняя будет являться квадратической средней величиной.
Аналогично, если по условиям задачи необходимо сохранить неизменной сумму кубов индивидуальных значений признака при их замене на среднюю величину, используют среднюю кубическую.
В статистической практике чаще, чем остальные виды средних взвешенных, используются средние арифметические и средние гармонические взвешенные. Средняя гармоническая имеет более сложную конструкцию, чем средняя арифметическая. Среднюю гармоническую применяют для расчетов тогда, когда в качестве весов используются не единицы совокупности – носители признака, а произведения этих единиц на значения признака (т.е. F = xf).
При определении средней величины в каждом конкретном случае нужно исходить из качественного содержания осредняемого признака, учитывать взаимосвязь изучаемых признаков, а также имеющиеся для расчета данные.
Расчет среднего значения качественного признака строится на основе его логической формуле. Под качественным признаком единицы совокупности, как правило, подразумеваются вторичные (расчетные) признаки (см. табл. 1.2), которые, в свою очередь, соответствуют относительным величинам интенсивности (см. табл. 4.1).
Правила выбора формы средней качественного признака:
1) если имеется ряд данных по двум взаимосвязанным показателям, для одного из которых нужно вычислить среднюю величину, и при этом известны численные значения знаменателя ее логической формулы, а значения числителя не известны, но могут быть найдены как произведение этих показателей, то средняя должна вычисляться по формуле средней арифметической взвешенной;
2) если в указанной постановке задачи известны численные значения числителя логической формулы, а значения знаменателя не известны, но могут быть найдены как частное от деления одного показателя на другой, то средняя должна вычисляться по формуле средней гармонической взвешенной;
3) в том случае, когда в условии задачи даны численные значения числителя и знаменателя логической формулы показателя, средняя вычисляется непосредственно по этой формуле.
 2014-01-25
2014-01-25 889
889








