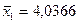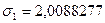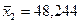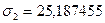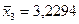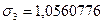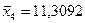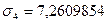Выявить конкурентные особенности российского рынка электротехнической промышленности, одно из пяти предприятий которого относится к Калининградскому региону (производство кабельной продукции). Каждое предприятие характеризуется следующими экономическими показателями: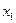 
- прибыль от реализации (млн. руб.); 
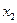- удельный вес высококачественной продукции (%); 
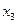- выработка товарной продукции на одного работника ППП (тыс. руб.); 
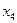- среднегодовая стоимость основных производственных фондов (млн. руб.).
Данные сведены в табл. 1.
Таблица 1 Значения основных экономических показателей предприятий электротехнической промышленности Северо-Западного региона России
| Номер
предприятия
| Показатели
|
|
|
|
|
|
|
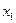
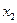
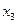
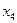
| 3,338
| 78,46
| 5,013
| 7,312
|
|
| 1,909
| 50,83
| 3,423
| 17,785
|
|
| 6,653
| 26,12
| 3,314
| 21,544
|
|
| 2,105
| 72,11
| 2,534
| 8,125
|
|
| 6,178
| 13,10
| 1,863
| 1,780
|
Таблица 1 и является исходной матрицей двумерной классификации. Для устранения различия в единицах измерения показателей нормируем их. В результате нормировки получаем приведенную матрицу исходных данных:
| -0,34776501
| 1,1996448
| 1,688891
| -0,55050379
| | -1,0591251
| 0,1026702
| 0,1833199
| 0,89186241
| | 1,3024511
| -0,8783738
| 0,0801078
| 1,4095607
| | -0,96155583
| 0,9475352
| -0,6584743
| -0,43853551
| | 1,0699948
| -1,3714763
| -1,2938443
| -1,3123838
|
| |
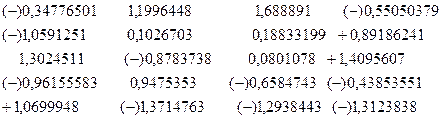
а также средние значения показателей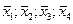 
и их средние квадратические отклонения:
В качестве расстояния между объектами принято евклидово расстояние, причем “веса”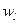 
заданы (путем привлечения экспертных оценок) пропорционально степени важности экономического показателя, например: 
.
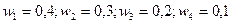Используя формулу рассчета эвклидовых расстояний с учетом “весовых” коэффициентов, рассчитываем матрицу расстояний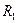 
, которая (в силу симметричности) представлена как треугольная.
|
| 1,159804
| 1,9283079
| 1,1311047
| 2,2980731
| | |
| 1,6262618
| 0,77977305
| 1,8968315
| | | |
| 1,9581917
| 1,1126867
| | | | |
| 1,9881173
| | | | | |
|
| |
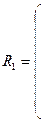
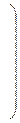
Из матрицы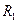 
следует, что объекты 2 и 4 наиболее близки (
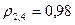) и поэтому возможно их объединение в один кластер, исходя из условия минимизации “расстояния”. После объединения имеем четыре кластера:
| Номера
кластера
|
|
|
|
|
 Состав
Кластера
| (1)
| (2,4)
| (3)
| (5)
|
Расстояние между кластерами будем находить по принципу “ближнего соседа”. За расстоянием между кластерами 1 и (2,4) выбираем минимальное из расстояни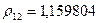й 
и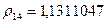 
. Аналогично находим расстояния между кластерами 2, 5 и (2,4), которые соответственно равны: 
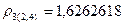и 
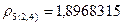. Расстояние между остальными кластерами можно считать не изменяющимися. Таким образом, получаем матрицу расстояний
|
| 1,1311047
| 1,9283079
| 2,2980731
| | |
| 1,6262618
| 1,8968315
| | | |
| 1,1126867
| | | | |
| | |
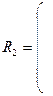
Из матрицы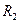 
следует, что кластеры 3 и 5 наиболее близки (
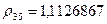) и поэтому объединяются в новый кластер (3,5). После объединения будем иметь три кластера 1, (2,4) и (3,5). Расстояния между новым кластером (3,5) и кластерами 1 и (2,4) соответственно равны: 
(
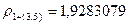меньше 
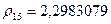) и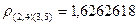 
. Поэтому матрица расстояний 
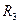принимает следующий вид:
|
| 1,1311047
| 1,9283079
| | |
| 1,6262618
| | | |
|
| |
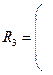
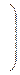
Из этой матрицы следует, что кластеры 1 и (2,4) объединяются в новый кластер (1+2,4), так как расстояние между ними минимально и равно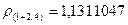 
.
Тогда получим матрицу расстояний
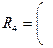
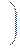
Таким образом, на расстоянии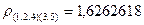 
два кластера (1,2,4) и (3,5) объединяются в один.
Результаты иерархической классификации наблюдений представлены на рис. 1 в виде дендрограммы, где по оси ординат приводятся относительные “расстояния” при объединении показателей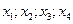 
работы предприятий с учетом “весовых” вкладов каждого параметра. Поэтому расстояния между исходными кластерами-предприятиями можно расценивать как конкурирующие факторы или факторы, необходимые для объединения в совместной деятельности с выгодой для себя и в ущерб остальным. Возможны и другие интерпретации, уровень которых зависит от квалификации и знания дела менеджером.
2015-05-22
320
