Совокупность частных критериев оптимальности 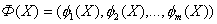 назовем векторным критерием оптимальности. Положим, что ставится задача максимизации каждого из указанных критериев в одной и той же области допустимых значений
назовем векторным критерием оптимальности. Положим, что ставится задача максимизации каждого из указанных критериев в одной и той же области допустимых значений 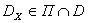 , где
, где 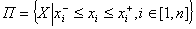 - «технологический» параллелепипед,
- «технологический» параллелепипед, 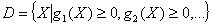 . Здесь
. Здесь 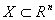 , где
, где 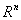 - n -мерное арифметическое пространство,
- n -мерное арифметическое пространство, 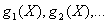 - ограничивающие функции. Задача многокритериальной оптимизации записывается в виде
- ограничивающие функции. Задача многокритериальной оптимизации записывается в виде
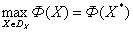 . (1)
. (1)
Запись (1) понимается лишь в том смысле, что для ЛПР желательна максимизация каждого из частных критериев.
Не формально, множество Парето можно определить как множество, в котором значение любого из частных критериев оптимальности можно улучшить (увеличить) только за счет ухудшения (уменьшения) хотя бы одного из остальных критериев. Т.е. любое из решений, принадлежащих множеству Парето, не может быть улучшено одновременно по всем частным критериям оптимальности.
Приведем формальное определение множества Парето. Векторный критерий оптимальности 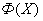 выполняет отображение множества
выполняет отображение множества 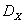 в некоторое множество
в некоторое множество 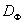 пространства критериев, которое называется множеством достижимости. Введем на множестве
пространства критериев, которое называется множеством достижимости. Введем на множестве 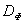 отношение предпочтения. Будем говорить, что вектор
отношение предпочтения. Будем говорить, что вектор 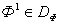 предпочтительнее вектора
предпочтительнее вектора 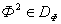 или вектор
или вектор 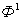 доминирует вектор
доминирует вектор 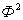 , и писать
, и писать 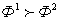 , если среди равенств и неравенств
, если среди равенств и неравенств 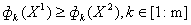 имеется хотя бы одно строгое неравенство. Выделим из множества
имеется хотя бы одно строгое неравенство. Выделим из множества 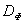 подмножество точек
подмножество точек 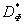 (фронт Парето), для которых нет более предпочтительных точек. Множество
(фронт Парето), для которых нет более предпочтительных точек. Множество 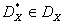 , соответствующее множеству
, соответствующее множеству 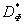 , называется множеством Парето. Таким образом, если
, называется множеством Парето. Таким образом, если 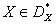 , то
, то 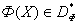 .
.
 2015-05-22
2015-05-22 369
369








