Подразумевается, что ученики знают все аксиомы, теоремы, свойства и формулы планиметрии и могут их использовать при решении задач в любой очерёдности вне зависимости от порядка их изучения.
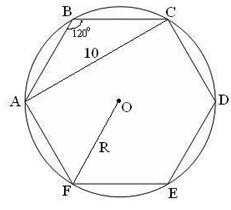
По данной задаче полагаем, что все знают, что 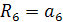 и внутренний угол правильного шестиугольника равен 120°. Эти факты в большей или меньшей степени мы использовали в разных способах решения задачи.
и внутренний угол правильного шестиугольника равен 120°. Эти факты в большей или меньшей степени мы использовали в разных способах решения задачи.
Ещё оговоримся, что доказательства очевидных фактов мы проводить не будем. Для простоты расчётов будем использовать следующий известный факт.
|
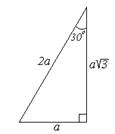
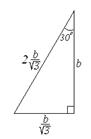
Если у прямоугольного треугольника с углом в 30° меньший катет обозначить через а, то гипотенуза будет 2а, катет равен 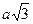 . .
|
|
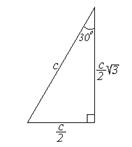
И наоборот. Если гипотенуза – с, то меньший катет – 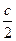 , а больший катет – , а больший катет – 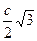 . .
|
|
А вот если известен больший катет – b, то меньший катет равен  , а гипотенуза равна , а гипотенуза равна 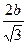 . .
|
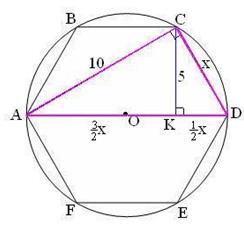
Рассмотрим разные способы решения одной задачи.
| 1. Формула связи стороны правильного треугольника и радиуса описанной около него окружности | |
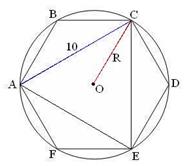
| Проведём отрезки AE и CE.
Получим правильный 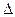 AEC.
Имеем AEC.
Имеем 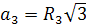 . Откуда . Откуда 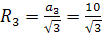 или или 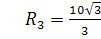 .
В дальнейшем ответ будем получать в виде .
В дальнейшем ответ будем получать в виде 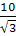 . .
|
| 2. Свойство пересечения медиан равностороннего треугольника | |
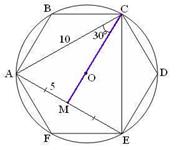
| В  ACE проведём медиану CM=m. ACE проведём медиану CM=m.
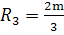 . В . В 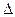 ACM ACM 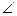 ACM=30°, AM=5, m= CM= ACM=30°, AM=5, m= CM= 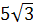 , ,
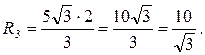
|
| 3. Равносторонний треугольник | |
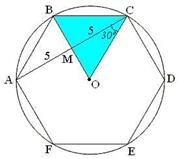
| Проведём отрезок ВО. Рассмотрим 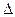 ВОС – равносторонний.
СМ= 5, ВОС – равносторонний.
СМ= 5, 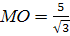 , , 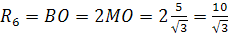 . .
|
| 4. Равнобедренный треугольник | |
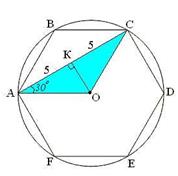
| Рассмотрим 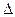 АСО - равнобедренный.
Проведём высоту ОК. Проведём ОА. АСО - равнобедренный.
Проведём высоту ОК. Проведём ОА.
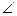 КАО= 30°, КАО= 30°, 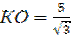 , ,
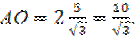
|
| 5. Прямоугольный треугольник | |
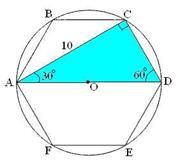
| Проведём АD.
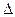 АСD - прямоугольный. АСD - прямоугольный.
 CAD=30°, CAD=30°, 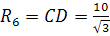 . .
|
| 6. Теорема Пифагора | |
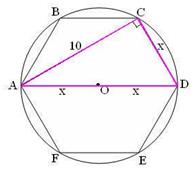
| В  ACD, ACD, 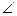 С= 90°. Обозначим CD= х, тогда AD= 2x.
По теореме Пифагора имеем С= 90°. Обозначим CD= х, тогда AD= 2x.
По теореме Пифагора имеем 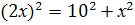 , ,
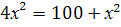 , , 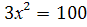 , ,
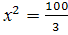 , х , х 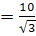 . Значит, . Значит, 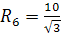 . .
|
| 7. Прямоугольник | |
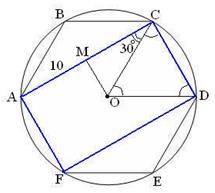
| Соеденим AF, FD, OD.
ACDF – прямоугольник.
Опустим перпендикуляр из точки О на сторону АС.
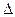 COD - правильный, COD - правильный, 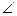 ОСМ= 30°.
МС= 5 см, ОСМ= 30°.
МС= 5 см,
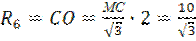 . .
|
| 8. Свойство диагоналей прямоугольника | |
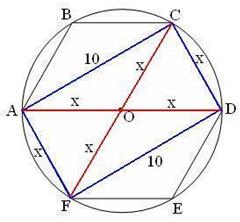
| ADCF – прямоугольник. AD и CF – диагонали прямоугольника.
Введём переменную х.
AO=OD=OC=OF=AF=CD=х,
AD=2х, CF=2х.
Используем свойство диагоналей прямоугольника. Составим уравнение.
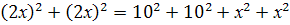
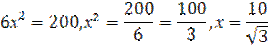 . .
|
| 9. Ромб | |
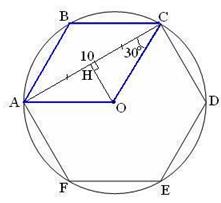
| Соединим А и О. АВСО – ромб.
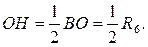 Рассмотрим Рассмотрим 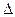 СОН, НС=5, СОН, НС=5, 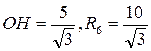 . .
|
| 10. Свойства диагоналей ромба | |
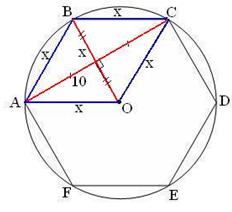
| АВСО – ромб.
Проведём диагонали АС и ВО.
Пусть АВ=ВС=СО=АО=ВО=х.
Тогда х2+х2+х2+х2=102+х2,
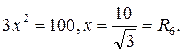
|
| 11. Равнобедренная трапеция | |
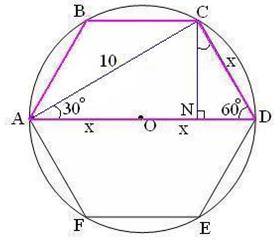
| ABCD – равнобедренная трапеция. CN – высота трапеции. 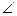 CAN=30o, CN=5. Пусть CD=x, тогда CAN=30o, CN=5. Пусть CD=x, тогда 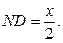
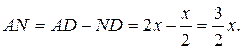
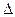 ACN – прямоугольный. Имеем ACN – прямоугольный. Имеем
 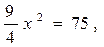
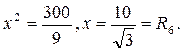
|
| 12. Прямоугольная трапеция | |
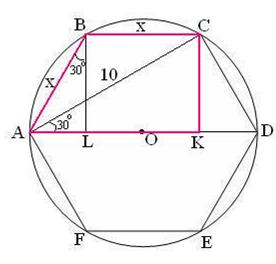
| Проведём AD. 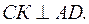 АВСК – прямоугольная трапеция.
BL – высота трапеции.
АВСК – прямоугольная трапеция.
BL – высота трапеции. 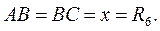 В
В 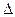 АСК АСК 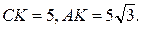 В
В 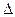 ABL ABL 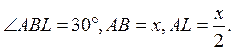 BC=LK=x. AL+LK=AK.
BC=LK=x. AL+LK=AK.
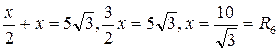 . .
|
| 13. Метод площадей. Ромб | |
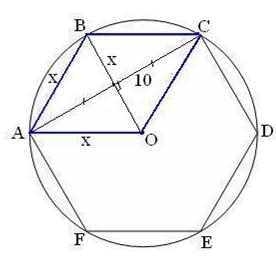
| ABCO – ромб. 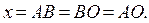
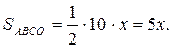
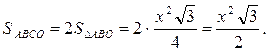 Приравняем правые части:
Приравняем правые части:
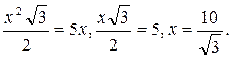
|
| 14. Метод площадей. Треугольник | |
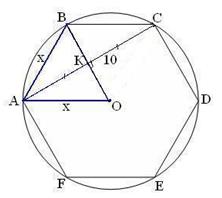
| Рассмотрим  АВО.
АВ=АО=ВО=х. АВО.
АВ=АО=ВО=х.  В
В 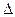 АОК АК=5, КО=х/2. АОК АК=5, КО=х/2.
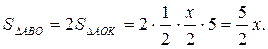
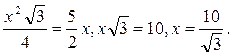
|
| 15. Метод площадей. Прямоугольник | |
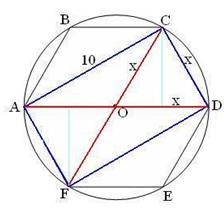
| ACDF – прямоугольник, CD=x.
 CO=OD=x. CO=OD=x.
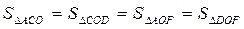 (равновеликие треугольники). (равновеликие треугольники).
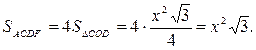
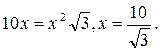
|
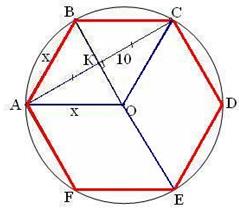
| 16. Метод площадей. Шестиугольник | |
| 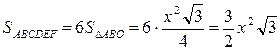 .
ABCO, CDEO, AFEO – равные ромбы. .
ABCO, CDEO, AFEO – равные ромбы.
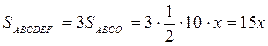 . .
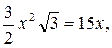 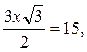 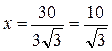 . .
|
| 17. Тригонометрический метод | |
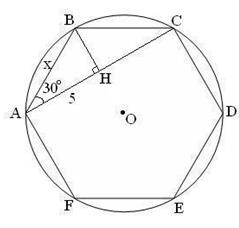
| 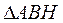 – прямоугольный. – прямоугольный. 

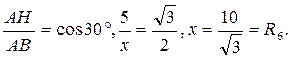
|
| 18. Теорема косинусов | |
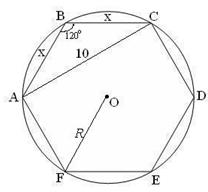
| 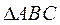 – равнобедренный. – равнобедренный.
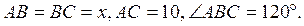
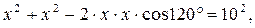
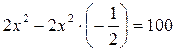 , ,
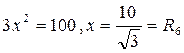 . .
|
| 19. Теорема синусов | |
| Из теоремы синусов имеем 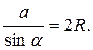 В
В 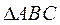 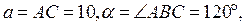
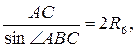 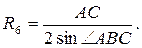
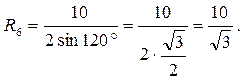
|
| 20. Метод подобия | |
| 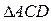 – прямоугольный. СК – высота, проведенная на гипотенузу.
Из – прямоугольный. СК – высота, проведенная на гипотенузу.
Из 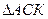 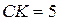 .
В .
В 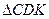 СD=x, СD=x, 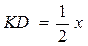 . .
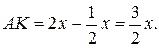 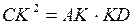 . .
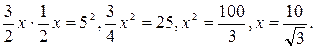
|
| 21. Радиус описанной окружности около треугольника | |
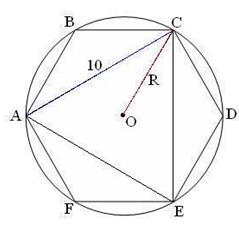
| Рассмотрим 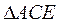 . АС=СЕ=АЕ=10.
По формуле . АС=СЕ=АЕ=10.
По формуле 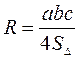 находим R6. находим R6.
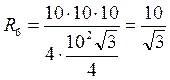 . .
|
| 22. Радиус вписанной окружности в треугольник | |
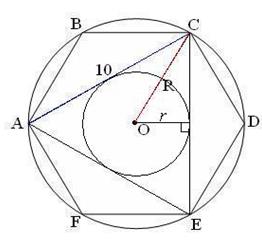
| В 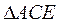 впишем окружность с радиусом r. впишем окружность с радиусом r. 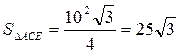 . .
 . .
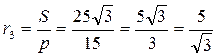 . .
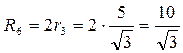 . .
|
| 23. Метод координат. Длина отрезка | |
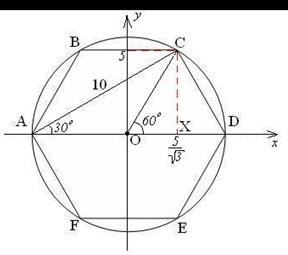
| Через точки А и D проведем ось Ох.
Чрез точку О перпендикулярно оси Ох проведем ось Оу. Из 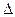 АСХ имеем СХ=5. Из АСХ имеем СХ=5. Из 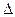 ОСХ имеем ОСХ имеем 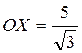 .
Значит, точка С имеет координаты .
Значит, точка С имеет координаты 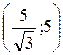 . . 
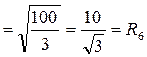
|
| 24. Метод координат. Середина отрезка | |
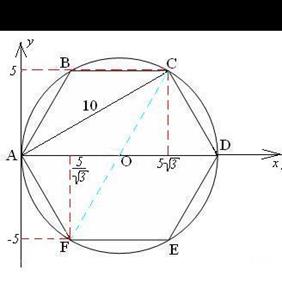
| Через точки А и D проведем ось Ох.
Чрез точку А перпендикулярно оси Ох проведем ось Оу. Точка С имеет координаты 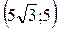 , а точка F –. , а точка F –. 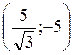 . Найдем координаты точки О – середины отрезка CF, заданного координатами концов. . Найдем координаты точки О – середины отрезка CF, заданного координатами концов. 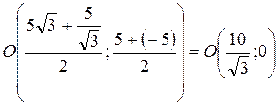 . Длина отрезка АО равна абсциссе точки О, т.е. . Длина отрезка АО равна абсциссе точки О, т.е. 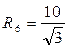 . .
|
| 25. Векторный метод | |
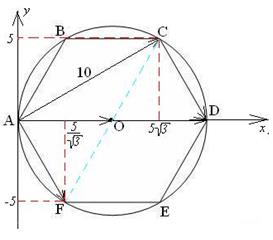
| Через точки А и D проведем ось Ох.
Чрез точку А перпендикулярно оси Ох проведем ось Оу.
Рассмотрим 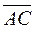 , ,  , , 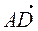 . .
 + + 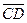 = = 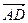 (по правилу треугольника) (по правилу треугольника)
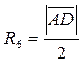 , , 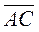 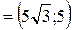 , ,
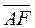 = =  , , 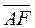 = = 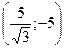 .
По правилу параллелограмма: .
По правилу параллелограмма:
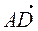 = = 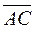 + + 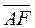 =
= =
= 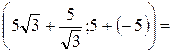 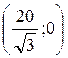 , ,
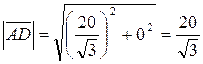 , , 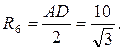 Можно найти
Можно найти 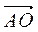 по формуле по формуле 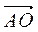 = = 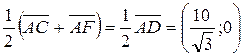 , ,
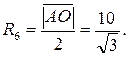
|
 2015-05-22
2015-05-22 230
230






