2015-06-10
5265Вариант 51. Теория вероятностей
Задача 1. В урне лежат 6 белых и 7 черных шаров. Наугад один за другим вынимают 2 шара (без возвращения). Какова вероятность того, что оба вынутые шара – белые?
Решение. Введем событие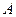 
= (Оба вынутые шара - белые). Используем классическое определение вероятности: 
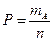, где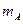 
– число исходов, благоприятствующих осуществлению события 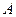, а n – число всех элементарных равновозможных исходов.
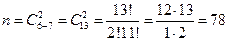- число различных способов выбрать 2 шара из имеющихся в урне 13 шаров.
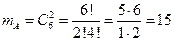- число различных способов выбрать 2 белых шара (из 6 белых шаров).
Вероятность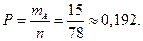 
Ответ: 0,192.
Задача 2. Какова вероятность того, что при одном бросании игральной кости выпадет нечетное число очков или число очков не больше 4?
Решение. Используем классическое определение вероятностей: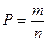 
, где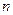 
– число всех равновозможных элементарных исходов, 
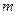– число элементарных исходов, благоприятствующих осуществлению события.
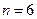- число различных выпадений кости (очков).
Перечислим благоприятные комбинации (нечетное число очков или число очков не больше 4): 1, 2, 3, 4, 5, поэтому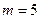 
Получаем вероятность: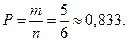 
Ответ: 0,833.
Задача 3. В первой урне 4 черных и 3 белых шара, во второй – 6 черных и 3 белых. Из одной из урн наугад достали шар. Найдите вероятность того, что этот шар – белый.
Решение. Введем полную группу гипотез:
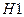= (Выбрана первая урна),
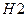= (Выбрана вторая урна).
Найдем вероятности гипотез по условию: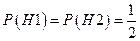 
.
Введем событие 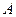= (Из урны вынут белый шар). Условные вероятности вычислим по формуле классической вероятности (отношение числа белых шаров к общему числу шаров в урне):
, 
.
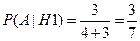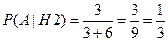Вероятность события 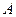найдем по формуле полной вероятности:
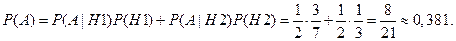
Ответ: 0,381.
Задача 4. Монетку бросают 6 раз. Найдите вероятность того, что ровно 3 раза выпадет «орел».
Решение. Имеем схему Бернулли с параметрами 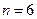(количество бросков монеты), 
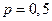(вероятность того, что выпадет «орел»), 
.
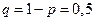Будем применять формулу Бернулли: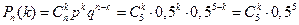 
- вероятность того, что из 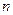монет «орлом» вверх выпали ровно 
.
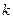Вероятность того, что ровно 3 раза выпадет «орел», равна:
.
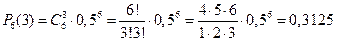Ответ: 0,3125.
Задача 5. Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,02. Поступило 200 вызовов. Определите вероятность «5 сбоев».
Решение. Имеем схему Бернулли с параметрами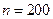 
, 
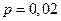. Так как 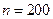достаточно велико, а вероятность 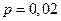мала, можно использовать для приближенного вычисления формулу Пуассона:
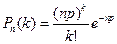- вероятность того, что из 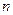вызовов будет ровно 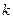«сбоев».
Обозначим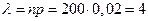 
, получим формулу 
.
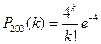Тогда вероятность того, что будет ровно 5 сбоев, равна
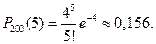
Ответ: 0,156.
Задача 6. Два стрелка поражают цель с вероятностями 0,6 и 0,3 соответственно. Первый стрелок сделал 1, а второй – 2 выстрела. Определите вероятность не менее двух попаданий в цель.
Решение. Введем независимые события
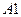= (Первый стрелок попал в цель),
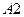= (Второй стрелок попал в цель),
в условии даны вероятности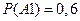 
, 
.
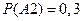Введем событие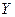 
= (Будет не менее двух попаданий в цель). Событие 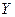произойдет если
или первый стрелок поразит цель, и второй поразит цель один раз,
или второй стрелок поразит цель два раза, а первый нет,
или второй стрелок поразит цель два раза, и первый тоже,
то есть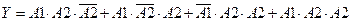 
. По теоремам сложения и умножения вероятностей получим
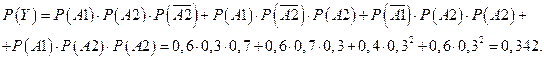
Ответ: 0,342.
Задача 7. Дан закон распределения случайной величины:
Найдите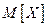 
, предварительно определив 
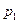, а также 
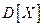и 
.
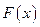Решение. Найдем 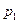из условия, что сумма вероятностей должна быть равна 1: 
.
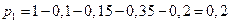Найдем математическое ожидание: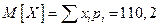 
.
Найдем дисперсию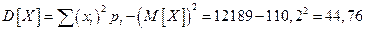 
Расчеты в таблице ниже:
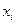 | Сумма | |||||
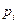 | 0,2 | 0,1 | 0,15 | 0,35 | 0,2 | |
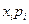 | 10,2 | 16,5 | 39,9 | 23,6 | 110,2 | |
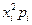 | 1040,4 | 4548,6 | 2784,8 |
Построим график функции распределения:
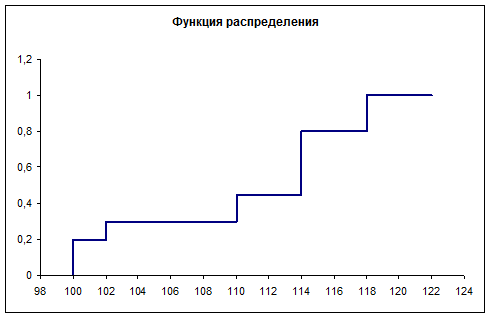
Задача 8. Случайные величины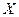 
и 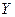независимы и распределены по нормальному закону с плотностями 
, 
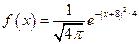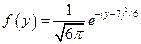. Найдите 
.
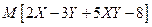Решение. По виду плотности распределения (сравнивая с каноническим видом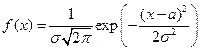 
), определяем, что параметр 
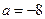, то есть 
.
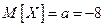По виду плотности распределения (сравнивая с каноническим видом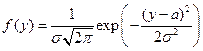 
), определяем, что параметр 
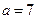, то есть 
.
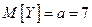Тогда
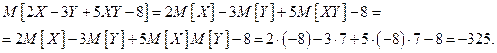
Ответ: -325.
Задача 9. Случайные величины 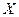и 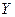независимы и распределены по нормальному закону с плотностями 
, 
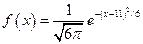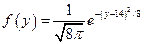. Найдите 
.
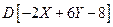Решение.
По виду плотности распределения (сравнивая с каноническим видом 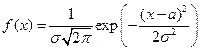), определяем, что параметр 
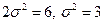, то есть 
.
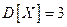По виду плотности распределения (сравнивая с каноническим видом 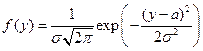), определяем, что параметр 
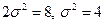, то есть 
.
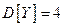Тогда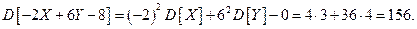 
Ответ: 156.
Задача 10. При каком значении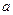 
функция
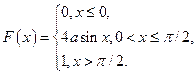будет функцией распределения некоторой непрерывной случайной величины ?
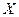Построить графики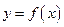 
и 
.
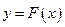Решение. По определению, должны выполняться равенства: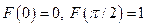 
. Подставляем и получаем:
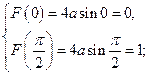
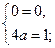
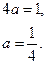
Значение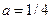 
.
Ответ: .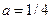
Задача 11. Пусть функция распределения случайной величины
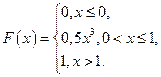
Найдите вероятность попадания значения случайной величины в интервал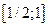 
.
Найти .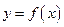
Решение. По определению, вероятность попадания значения случайной величины в интервал 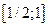можно найти как приращение функции распределения на этом интервале:
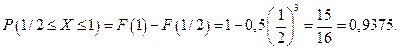
Найдем плотность распределения как производную от функции распределения:
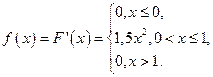
Ответ: 0,9375.
Задача 12. Пусть функция распределения случайной величины
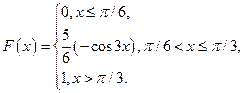
Найдите плотность распределения вероятностей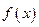 
случайной величины Х. В ответе укажите значение 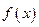при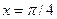 
.
Решение. По определению, плотность можно найти как производную от функции распределения:
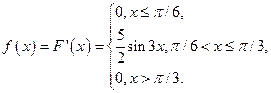
Тогда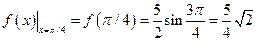 
.
Ответ: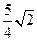 
.
ЛИТЕРАТУРА
- Вентцель Е.С. Теория вероятностей.-М.: Наука, 1969.-576 с.
- Гмурман В.Е. Теория вероятностей и математическая статистика.-М.: Высшая школа, 2001.-479 с.
- Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике.-М.: Высшая школа, 2001.-400 с.
