Пуассоновский процесс

Пусть

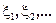
последовательность независимых одинаково распределенных случайных величин, имеющих экспоненциальное распределение с параметром

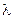
Случайная последовательность точек

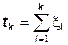
на неотрицательной полуоси называется пуассоновский (точечный) процесс.

Вычислим распределение числа точек

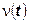
пуассоновского процесса в интервале (0,t)

События

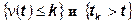
эквиваленты, поэтому

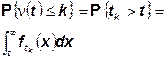
Но распределение случайной величины

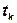
является распределением Эрланга порядка k, поэтому

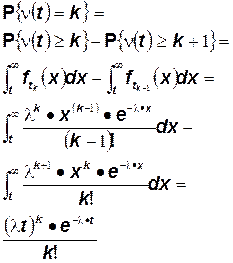
Таким образом распределение количества точек пуассоновского процесса в интервале (o,t) это пуассоновское распределение с параметром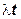

Пуассоновский процесс используется для моделирования моментов наступления случайных событий – процесса радиоактивного распада, моментов поступления звонков на телефонную станцию, моментов появления клиентов в системе обслуживания, моментов отказа оборудования.