Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона

Пусть эмпирическое распределение задано в виде последовательности равноотстоящих вариант 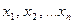и соответствующих им частот 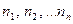. Требуется, используя критерий Пирсона, проверить гипотезу о том, что генеральная совокупность распределена нормально.

Для того чтобы при заданном уровне значимости 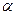проверить гипотезу о нормальном распределении генеральной совокупности, надо:

1. Вычислить выборочную среднюю 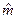и выборочное среднее квадратическое отклонение .

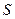2. Вычислить теоретические частоты

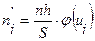, (5)

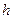где - объем выборки, - длина интервала,

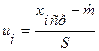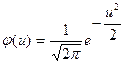, (по таблице).

3. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона. Для этого:

а) составим расчетную таблицу,

			-

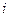
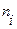
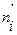
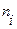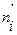
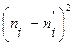
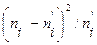
по которой находим наблюдаемое значение критерия

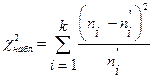; (6)

б) по таблице критических точек распределения 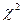, по данному уровню значимости 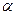и числу степеней свободы 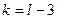( 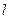- число групп выборки) находят критическую точку 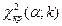правосторонней критической области.

Если 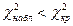, то нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности, т.е. эмпирические и теоретические частоты различаются незначимо (случайно). Если же 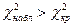- гипотезу отвергают, т.е. эмпирические и теоретические частоты различаются значимо.