При обработке опытных данных часто приходится решать задачу, в которой необходимо установить или исследовать функциональную зависимость одной величины от другой на основании полученных данных.
Пусть производится опыт с целью исследования зависимости величины 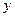 от величины
от величины  , которая в общем случае может быть записана в виде
, которая в общем случае может быть записана в виде
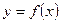 .
.
Требуется установить вид этой зависимости на основании опытных данных.
Предположим, что в результате опыта получен набор точек 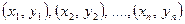 и построен обобщенный график зависимости, т.е. линия, построенная не точно по точкам
и построен обобщенный график зависимости, т.е. линия, построенная не точно по точкам 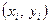 , а линия, сглаживающая разброс точек, который связан со случайными ошибками измерений. Задача заключается в такой обработке данных, при которой по возможности точно была бы отражена тенденция зависимости
, а линия, сглаживающая разброс точек, который связан со случайными ошибками измерений. Задача заключается в такой обработке данных, при которой по возможности точно была бы отражена тенденция зависимости 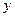 от
от  и возможно полнее исключено влияние случайных, незакономерных уклонений, связанных с погрешностями опыта. Такая задача называется задачей сглаживания экспериментальной зависимости, т.е. изображения опытной функциональной зависимости аналитической формулой.
и возможно полнее исключено влияние случайных, незакономерных уклонений, связанных с погрешностями опыта. Такая задача называется задачей сглаживания экспериментальной зависимости, т.е. изображения опытной функциональной зависимости аналитической формулой.
При решении такой задачи в случае, когда вид зависимости 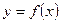 до опыта известен, обычно применяется расчетный метод – метод наименьших квадратов.
до опыта известен, обычно применяется расчетный метод – метод наименьших квадратов.
Суть метода:
Пусть получено  экспериментальных точек с абсциссами
экспериментальных точек с абсциссами 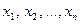 и ординатами
и ординатами 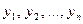 .
.
Зависимость 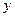 от
от  , изображаемая аналитической функцией
, изображаемая аналитической функцией
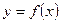 (1)
(1)
не может совпадать с экспериментальными значениями 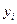 во всех
во всех  точках. Это означает, что для всех или некоторых точек разность
точках. Это означает, что для всех или некоторых точек разность
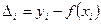 (2)
(2)
будет отлична от нуля.
Требуется подобрать параметры функции (1) таким образом, чтобы сумма квадратов разностей (2) была наименьшей, т.е. требуется обратить в минимум выражение
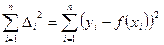 (3)
(3)
Таким образом, по методу наименьших квадратов приближенное значение аналитической функции 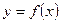 к экспериментальной зависимости считается наилучшим, если выполняется условие минимума суммы квадратов отклонений искомой аналитической функции от экспериментальной зависимости.
к экспериментальной зависимости считается наилучшим, если выполняется условие минимума суммы квадратов отклонений искомой аналитической функции от экспериментальной зависимости.
Следует заметить, что выражение (3) представляет собой полином второй степени относительно неизвестных параметров (причем неизвестные параметры в зависимость 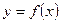 входят линейно), который не может принимать отрицательных значений. Поэтому существуют такие значения неизвестных параметров, при которых функция (3) достигает минимума, и этот минимум в зависимости от значений
входят линейно), который не может принимать отрицательных значений. Поэтому существуют такие значения неизвестных параметров, при которых функция (3) достигает минимума, и этот минимум в зависимости от значений 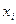 и
и 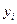 будет положительным или равным нулю.
будет положительным или равным нулю.
Так как неизвестные параметры в зависимость 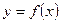 входят линейно, будем искать эту зависимость в виде
входят линейно, будем искать эту зависимость в виде
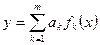 , (4)
, (4)
где 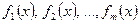 - известные функции, а
- известные функции, а 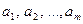 - неизвестные параметры.
- неизвестные параметры.
Исходя из принципа наименьших квадратов, мы должны подобрать такие значения неизвестных параметров 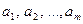 , при которых обращается в минимум выражение
, при которых обращается в минимум выражение
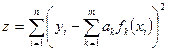 (5)
(5)
Это выражение является функцией неизвестных параметров 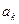 , поэтому для отыскания минимума функции нужно согласно правилам дифференциального исчисления найти частные производные функции
, поэтому для отыскания минимума функции нужно согласно правилам дифференциального исчисления найти частные производные функции 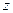 по всем параметрам
по всем параметрам 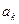 и приравнять их к нулю:
и приравнять их к нулю:
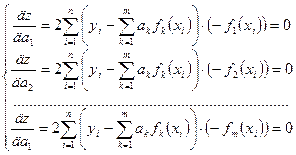 (7)
(7)
Подставляя в систему опытные значения 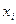 и
и 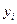 , получим систему
, получим систему 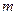 линейных уравнений относительно неизвестных параметров
линейных уравнений относительно неизвестных параметров 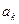 , решение которой может быть получено с помощью определителей или методом Гаусса.
, решение которой может быть получено с помощью определителей или методом Гаусса.
Рассмотрим применение метода наименьших квадратов, когда для изображения экспериментальной зависимости выбрана парабола
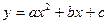 .
.
Пусть в результате независимых опытов получено  значений величины
значений величины 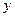 :
:
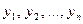 ,
,
соответствующих значениям величины 
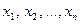 .
.
Для определения неизвестных параметров 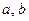 и
и 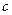 методом наименьших квадратов составляем сумму квадратов отклонений искомой аналитической функции от наблюдаемых значений в данных точках
методом наименьших квадратов составляем сумму квадратов отклонений искомой аналитической функции от наблюдаемых значений в данных точках
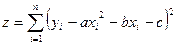 (8)
(8)
Дифференцируя функцию (8) по неизвестным параметрам 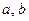 и
и 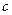 , и приравнивая производные к нулю, получим следующую систему уравнений:
, и приравнивая производные к нулю, получим следующую систему уравнений:
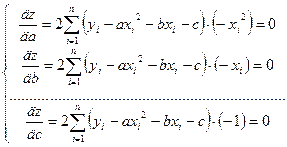 или
или 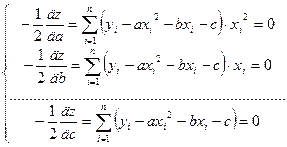
Или, после преобразований:
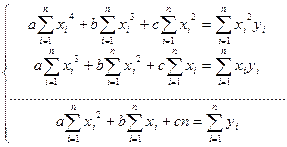 . (9)
. (9)
Система (9) представляет собой СЛАУ относительно неизвестных параметров 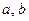 и
и 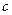 . Решая методом Гаусса находим эти значения.
. Решая методом Гаусса находим эти значения.
 2015-06-10
2015-06-10 1786
1786