Специальность: 5В050800 – Финансы, 5В050600 – Экономика, 5В050900 – Учет и аудит
Семестр: 2; курс: 1; группы: БУА-12, БФ-12, БЭК-12
Язык обучения: русский
Преподаватель ответственный за разработку тестов: Уланов Борис Васильевич.
| № п.п | Уровень сложности | Вопросы | Раздел Тема | A) (Правильный ответ) | B) | C) | D) | E) | |
| 1. | Под событием понимают такой результат эксперимента или наблюдения, который при реализации данного комплекса условий может: | Произойти или не произойти | Произойти | не произойти | Обязательно произойти | Неизбежно произойти | |||
| 2. | Какое событие называют достоверным? | Которое неизбежно произойдет при определенном комплексе условий | Которое не может произойти при определенном комплексе условий | Которое может либо произойти, либо нет | Это результат эксперимента… | Любое событие | |||
| 3. | Какое событие называют невозможным? | Которое не может произойти при определенном комплексе условий | Которое неизбежно произойдет при определенном комплексе условий | Которое может либо произойти, либо нет | Это результат эксперимента… | Любое событие | |||
| 4. | Какое событие называют случайным? | Которое при испытании может либо произойти, либо нет | Которое не может произойти при определенном комплексе условий | Которое неизбежно произойдет при определенном комплексе условий | Это результат эксперимента… | Любое событие | |||
| 5. | Укажите формулу классического определения вероятности | Р(А)=m/n | W(A)=m/n | A 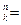 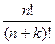 | C 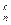 = = 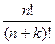 | P 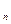 =n! =n! | |||
| 6. | Укажите формулу по которой вычисляется относительная частота | W(A)=m/n | Р(А)=m/n | A 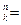 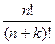 | C 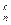 = = 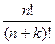 | P 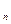 =n! =n! | |||
| 7. | Вероятность достоверного события равна: | 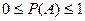 | 0,1 | ||||||
| 8. | Вероятность невозможного события равна: | 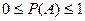 | 0,1 | ||||||
| 9. | Вероятность случайного события Р(А) удовлетворяет неравенствам…: | 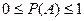 | 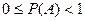 | 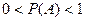 | 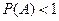 | 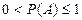 . . | |||
| 10. | Найдите формулу с помощью которой находятся перестановки из n различных элементов: | P 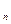 =n! =n! | A 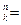 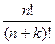 | C 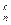 = = 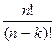 | C 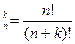 | P 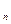 =n =n | |||
| 11. | Найдите формулу с помощью которой находится число размещений из n элементов по k элементов: | A 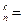 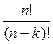 | C 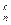 = = 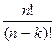 | C 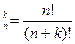 | P 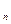 =n! =n! | A 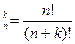 | |||
| 12. | Найдите формулу с помощью которой находится число сочетаний из n элементов по k элементов: | 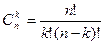 | A 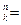 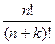 | C 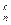 = = 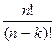 | C 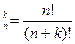 | P 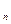 =n! =n! | |||
| 13. | Сколько трехзначных чисел можно составить из чисел 1,2,3, если каждая цифра входит в изображение числа только один раз? | ||||||||
| 14. | Сколько трехзначных чисел можно составить из чисел 1,2,3,4,5 без повторений? | ||||||||
| 15. | Число всех сочетаний из семи элементов по три равно: | ||||||||
| 16. | Сколькими способами можно выбрать 2 детали из ящика, содержащего 10деталей. | ||||||||
| 17. | Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра. | 1/10 | 1/2 | 1/5 | |||||
| 18. | Брошена игральная кость. Найти вероятность того, что выпадет четное число очков. | 0,5 | 0,4 | 0,2 | |||||
| 19. | Игральная кость подбрасывается один раз. Найти вероятность того, что выпадет число очков равное шести. | 1/6 | 1/2 | 1/3 | 1/4 | ||||
| 20. | Подбрасываются две игральные кости. Найти вероятность того, что число очков на игральных костях совпадает. | 1/6 | 1/2 | 1/36 | 5/6 | ||||
| 21. | Подбрасываются две игральные кости. Найти вероятность того, что число очков на первой кости больше, чем на второй. | 5/12 | 1/6 | 1/36 | 2/3 | 1/3 | |||
| 22. | В партии из 100 деталей отдел технического контроля обнаружил 5 нестандартных деталей. Чему равна относительная частота появления нестандартных деталей? | 0,05 | 0,03 | 0,01 | 0,5 | 0,6 | |||
| 23. | Известно, что всхожесть семян пшеницы 90 %. Сколько необходимо взять зерен, чтобы взошло 360 растений. | ||||||||
| 24. | Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5? | 0,81 | 0,8 | 0,2 | 0,15 | 0,35 | |||
| 25. | В мешочке имеется 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: о, п, р, с, т. Найти вероятность того, что на вынутых по одному и расположенных в одну линию кубиков можно будет прочесть слово «спорт» | 1/120 | 1/12 | 1/25 | 1/5 | 1/32 | |||
| 26. | Из слова «студент» случайным порядком выбирают букву. Какова вероятность, что выбранной окажется гласная буква: | 2/7 | 1/2 | 2/5 | 1/3 | 2/3 | |||
| 27. | Найти вероятность того, что наудачу выбранное из отрезка 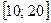 двузначное число делится на 2: двузначное число делится на 2: | 6/11 | 3/11 | 2/11 | 5/11 | 1/11 | |||
| 28. | Найти вероятность того, что карта вынутая из колоды в 36 карт, окажется тузом: | 1/9 | 1/2 | 1/4 | 1/3 | 1/6 | |||
| 29. | Брошены три монеты. Найти вероятность того, что выпадут два «герба» | 3/8 | 1/2 | 1/4 | |||||
| 30. | Точка взята наудачу внутри круга радиуса R. Найти вероятность того, что эта точка окажется от центра на расстоянии, меньшем r (r<R). | (r/R)2 | r/R2 | r/R | r2 | (rR)2 | |||
| 31. | На отрезке длины 20 см помещен меньший отрезокдлины 10 см. Найти вероятность того, что точка наудачу поставленная на больший отрезок, попадет также и на меньший отрезок. предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения. | 1/2 | 1/3 | ||||||
| 32. | Пусть в результате испытания ожидаются события А и В. Сумма этих событий, А+В, означает: | появится или А, или В, или оба эти события | появится В, но не появится А | появится А, но не появится В | появится и А, и В | обязательно появится одно из них | |||
| 33. | Пусть в результате испытания ожидаются события А и В. Произведение этих событий, АВ, означает: | появится и А, и В | появится или А, или В | появится хотя бы одно из них | появится одно из них | появится А без В или В без А | |||
| 34. | Если события А и В несовместны, то p(A+B)=: | p(A)+p(B) | p(A)-p(B) | p(A)/p(B) | p(A)ּp(B) | ||||
| 35. | Если события А и В независимы, то p(AB)=: | p(A)ּp(B) | p(A)/p(B) | p(A)+p(B) | p(A)-p(B) | ||||
| 36. | Формула вероятности противоположного события: | 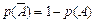 | 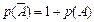 | 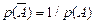 | 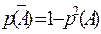 | 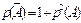 | |||
| 37. | Если 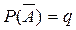 , то Р(А)= , то Р(А)= | 1-q | 1-p | p+q | q+1 | p+1 | |||
| 38. | Противоположными называются: | два единственно возможных события, образующих полную группу | два достоверных события | два невозможных события | два случайных события | результат некоторого эксперимента | |||
| 39. | Условной вероятностью 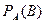 называют: называют: | вероятность события В, вычисленную в предположении, что событие А уже наступило | вероятность события А, вычисленную в предположении, что событие В уже наступило | два единственно возможных события, образующих полную группу | вероятность события В | вероятность события А | |||
| 40. | Полная вероятность вычисляется по формуле Р(А)=: | 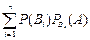 | 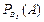 | 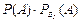 | 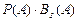 | 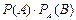 | |||
| 41. | Формула Бейеса 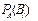 =: =: | 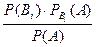 | 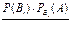 | 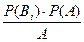 | 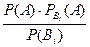 | 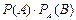 | |||
| 42. | Вероятность того, что день будет ясным р=0,7. Найти вероятность того, что день будет дождливым: | 0,3 | 0,4 | 0,5 | 0,6 | 0,2 | |||
| 43. | Предстоит опыт: из колоды 36 карт будет вынута одна. Какова вероятность того, что эта карта - туз или король? | 2/9 | 1/9 | 24/36 | 1/18 | 1/2 | |||
| 44. | В ящике 4 белых, 5 красных, 8 зеленых и 3 голубых шара. Шары перемешивают и извлекают один шар. Какова вероятность события, состоящего в том, что шар окажется цветным? | 4/5 | 1/5 | 5/8 | 3/20 | 1/2 | |||
| 45. | В цехе работают 2 транспортера. Вероятность безотказной работы за время t каждого из них равна 0,9. Транспортеры работают независимо друг от друга. Найти вероятность того, что за время t будут работать хотя бы один транспортер. | 0,99 | 0,81 | 0,01 | 0,18 | 0,1 | |||
| 46. | В цехе работают 2 транспортера. Вероятность безотказной работы за время t каждого из них равна 0,9. Транспортеры работают независимо друг от друга. Найти вероятность того, что за время t будут работать оба транспортера. | 0,81 | 0,99 | 0,01 | 0,18 | 0,1 | |||
| 47. | В цехе работают 2 транспортера. Вероятность безотказной работы за время t каждого из них равна 0,9. Транспортеры работают независимо друг от друга. Найти вероятность того, что за время t не будет работать ни один транспортер. | 0,01 | 0,81 | 0,99 | 0,18 | 0,1 | |||
| 48. | В цехе работают 2 транспортера. Вероятность безотказной работы за время t каждого из них равна 0,9. Транспортеры работают независимо друг от друга. Найти вероятность того, что за время t будет работать только один транспортер. | 0,18 | 0,01 | 0,81 | 0,99 | 0,1 | |||
| 49. | Устройство состоит из трех элементов, работающих независимо. Вероятность безотказной работы за время t первого, второго и третьего элементов соответственно равны 0,6; 0,7; 0,8. Найти вероятности того, что за время t безотказно будут работать только один элемент. | 0,188 | 0,452 | 0,336 | 0,1 | 0,01 | |||
| 50. | Устройство состоит из трех элементов, работающих независимо. Вероятность безотказной работы за время t первого, второго и третьего элементов соответственно равны 0,6; 0,7; 0,8. Найти вероятности того, что за время t безотказно будут работать только два элемент. | 0,452 | 0,188 | 0,336 | 0,236 | ||||
| 51. | Устройство состоит из трех элементов, работающих независимо. Вероятность безотказной работы за время t первого, второго и третьего элементов соответственно равны 0,6; 0,7; 0,8. Найти вероятности того, что за время t безотказно будут работать все три элемента. | 0,336 | 0,452 | 0,188 | 0,25 | 0,1 | |||
| 52. | Вероятность попадания в цель р=0,9. Определить вероятность того, что при 3 выстрелах будет 3 попадания. | 0,729 | 0,9 | 0,81 | 0,1 | ||||
| 53. | Найти вероятность появления 2 «гербов» при одном подбрасывании 2 монет: | 1/4 | 1/2 | 1/6 | 1/3 | ||||
| 54. | 2 стрелка стреляют по очереди. Вероятность попадания в цель первого стрелка 0,9, второго – 0,8. Найти вероятность попадания хотя бы одного стрелка. | 0,98 | 0,963 | 0,369 | 0,396 | 0,983 | |||
| 55. | В студии телевидения три телекамеры. Для каждой камеры вероятность того, что она включена в данный момент, равна 0,6. Найти вероятность того, что в данный момент включена хотя бы одна камера. | 0,936 | 0,963 | 0,369 | 0,396 | 0,983 | |||
| 56. | Два стрелка стреляют по очереди Вероятность попадания в цель первого стрелка 0,7, а второго 0,8. Найти вероятность попадания хотя бы одного стрелка: | 0,94 | 0,9 | 0,92 | 0,97 | ||||
| 57. | С первого станка на сборку поступает 40%, со второго – 30%, с третьего – 20%, с четвертого – 10% всех деталей. Среди деталей первого станка 0,1% бракованных, второго – 0,2%, третьего -0,25%, четвертого – 0,5%. Найти вероятность того, что поступившая на сборку деталь - бракованная. | 0,002 | 0,02 | 0,2 | |||||
| 58. | Для участия в студенческих отборочных соревнованиях выделено из первой группы курса 4, из второй – 6, из третьей – 5 студентов. Вероятности того, что студент 1,2,3 группы попадет сборную института, соответственно равны 0,9; 0,7; 0,8. Наудачу выбранный студент в итоге соревнования попал в сборную. Найти вероятность того, что студент попал в сборную. | 59/75 | 4/150 | 7/150 | 8/150 | ||||
| 59. | В ящике 12 деталей изготовленных на заводе №1, 20 деталей изловленных на заводе №2, 18 деталей изловленных на заводе №3. Вероятность того, что деталь изготовлена на заводе №1 отличного качества, равна 0,9; для деталей изготовленных на заводе №2,3 эти вероятности соответственно равны 0,6 и 0,9. Найти вероятность того, что извлеченная наудачу деталь окажется отличного качества. | 0,78 | 0,24 | 0,4 | 0,36 | 0,87 | |||
| 60. | Вероятности того, что во время работы цифровой электронной машины произойдет сбой в арифметическом устройстве, в оперативной памяти, в остальных устройствах, относятся как 3:2:5. Вероятности обнаружения сбоя в арифметическом устройстве, в оперативной памяти, в остальных устройствах соответственно равны 0,8; 0,9; 0,9. Найти вероятность того, что возникший в машине сбой будет обнаружен. | 0,87 | 0,78 | 0,9 | 0,8 | ||||
| 61. | В пирамиде 5 винтовок, 3 из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического эта вероятность будет равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки. | 0,85 | 0,95 | 0,7 | |||||
| 62. | Среди 100 лотерейных билетов есть 5 выигрышных. Найти вероятность того, что 2 наудачу выбранные билета окажутся выигрышными. | 1/495 | 1/2 | 1/120 | 1/5 | 1/100 | |||
| 63. | В читальном зале имеется 6 учебников по теории вероятности, из которых 3 в переплете. Библиотекарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в переплете. | 0,2 | 0,1 | 0,5 | 0,3 | 0,6 | |||
| 64. | Брошены монета и игральная кость. Найти вероятность того, что выпадут «орел» и «6 очков»: | 1/12 | 1/3 | 1/6 | 1/2 | 1/4 | |||
| 65. | В цехе работают 20 станков. Из них 10 марки А, 6 марки Б и 4 марки С. Вероятность того, что качество детали окажется отличным, для этих станков соответственно равна: 0,9, 0,8, 0,7. Какой процент отличных деталей выпускает цех в целом? | 83% | 30% | 10% | 20% | ||||
| 66. | На фабрике, изготовляющей болты, первая машина производит 25%, вторая 35%, третья 40% всех изделий. В их продукции брак составляет соответственно 5%, 4% и 2%. Какова вероятность того, что случайно выбранный болт дефектный? | 0,0345 | 0,36 | 0,39 | 0,25 | 0,65 | |||
| 67. | На фабрике, изготовляющей болты, первая машина производит 25%, вторая 35%, третья 40% всех изделий. В их продукции брак составляет соответственно 5%, 4% и 2%. Случайно выбранный из продукции болт оказался дефектным. Какова вероятность того, что он был произведен первой машиной? | 125/345 | 140/345 | 124/346 | 120/345 | ||||
| 68. | На фабрике, изготовляющей болты, первая машина производит 25%, вторая 35%, третья 40% всех изделий. В их продукции брак составляет соответственно 5%, 4% и 2%. Случайно выбранный из продукции болт оказался дефектным. Какова вероятность того, что он был произведен второй машиной? | 140/345 | 125/345 | 80/345 | |||||
| 69. | На фабрике, изготовляющей болты, первая машина производит 25%, вторая 35%, третья 40% всех изделий. В их продукции брак составляет соответственно 5%, 4% и 2%. Случайно выбранный из продукции болт оказался дефектным. Какова вероятность того, что он был произведен третьей машиной? | 80/345 | 125/345 | 80/347 | |||||
| 70. | Определить вероятность того, что в семье, имеющей 5 детей будет 3 девочки и 2 мальчика. Вероятности рождения мальчика и девочки предполагаются одинаковыми. | 5/16 | 1/16 | 2/5 | 3/5 | 4/5 | |||
| 71. | Монету подбрасывают 8 раз. Какова вероятность того, что 6 раз она упадет гербом вверх? | 7/64 | 8/65 | 1/16 | 2/5 | 6/8 | |||
| 72. | В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в данный момент включен 4 мотора. | 0,246 | 0,254 | 0,256 | 0,25 | 0,369 | |||
| 73. | Вероятность того, что стрелок при одном выстреле попадает в мишень, равна р=0,9. Стрелок произвел 3 выстрела. Найти вероятность того, что все 3 выстрела дали попадание. | 0,729 | 0,81 | 0,72 | 0,25 | 0,504 | |||
| 74. | В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в данный момент включены все моторы | 0,26 | 0,246 | 0,254 | 0,000064 | 0,62 | |||
| 75. | В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в данный момент выключены все моторы: | 0,000064 | 0,00064 | 0,0000064 | 0,0064 | 0,64 | |||
| 76. | Формула Бернулли 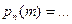 : : | 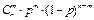 | 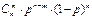 | 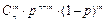 | 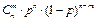 | 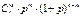 | |||
| 77. | Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25. (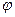 (1,37)=0,1561) (1,37)=0,1561) | 0,0231 | 0,028 | 0,2 | 0,1 | 0,25 | |||
| 78. | Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз (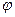 (1,25)=0,1826) (1,25)=0,1826) | 0,04565 | 0,02 | 0,05 | 0,36 | 0,1 | |||
| 79. | Случайная величина называется дискретной, если число принимаемых ею значений: | конечно или счетно | конечно | счетно | ограничено | ограничено, но счетно | |||
| 80. | Случайной величиной называют величину, которая в результате испытания может: | принимать те или иные значения, в зависимости от различных обстоятельств | непринимать изолированные значения | принимать изолированные значения | зависеть от обстоятельств | не принимать те значения | |||
| 81. | Дискретной случайной величиной называют величину: | возможные значения, которой есть отдельные изолированные числа с определенными вероятностями | возможные значения, которой числа | которая в результате испытания может принимать значения | возможные значения, которой есть вероятности | возможные значения, которой есть отдельные числа | |||
| 82. | Законом распределения дискретной случайной величины называют: | перечень ее возможных значений и соответствующих им вероятностей | перечень ее возможных значений | перечень ее возможных вероятностей | перечень ее вероятностей | перечень ее значений | |||
| 83. | Формула Пуассона Pn(k)=: | 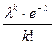 | 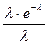 | 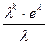 | 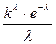 | 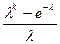 | |||
| 84. | Числовыми характеристиками вариационного ряда являются: | М(Х), Д(Х), 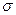 (Х) (Х) | М(Х) | М(Х), Д(Х) | Д(Х), 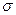 (Х) (Х) | 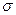 (Х) (Х) | |||
| 85. | Математическим ожиданием ДСВ называется: | сумма произведений всех ее значений на соответствующие им вероятности | произведений всех ее значений | сумма всех вероятностей | произведение всех ее значений и вероятностей | сумма всех ее значений | |||
| 86. | Математическое ожидание ДСВ обладает свойством М(СХ)=: | 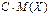 | 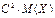 | 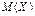 | 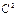 | С | |||
| 87. | Математическое ожидание ДСВ обладает свойством М(Х+У+Z)= | М(Х) + M(У) + M(Z) | М(Х)+M(У) | 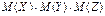 | М(Х) - M(У) - M(Z) | М(Х)-M(У) | |||
| 88. | Математическое ожидание ДСВ обладает свойством 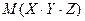 = = | 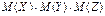 | М(Х) + M(У) + M(Z) | 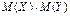 | М(Х) - M(У) - M(Z) | 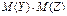 | |||
| 89. | Дисперсия Д(Х) ДСВ вычисляется по формуле: | 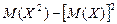 | 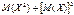 | 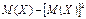 | 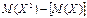 | 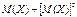 | |||
| 90. | Дисперсия ДСВ обладает свойством Д(СХ)=: | 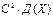 | 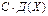 | 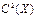 | 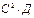 | 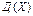 | |||
| 91. | Дисперсия ДСВ обладает свойством Д(Х+У+Z)= | Д(Х) + Д(У) + Д(Z) | Д(Х) | Д(Х) - Д(У) | Д(У) + Д(Z) | Д(Х+Z) | |||
| 92. | Дисперсия ДСВ обладает свойством Д(Х-У)= | Д(Х) + Д(У) | Д(Х)-Д(У) | Д(У) + Д(Z) | Д(Х) + Д(У) + Д(Z) | Д(Х+Z) | |||
| 93. | Среднее квадратическое отклонение вычисляют по формуле: | 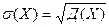 | 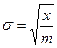 | 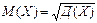 | 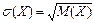 | 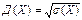 | |||
| 94. | Математическое ожидание числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна: | М(Х)=np | М(Х)=npq | Д(Х)=npq | М(Х)=nq | М(Х)=pq | |||
| 95. | Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна: | Д(Х)=npq | Д(Х)=pq | M(Х)=npq | Д(Х)=n+p+q | Д(Х)=n-p-q | |||
| 96. | Функцией распределения называют функцию: | 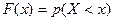 | 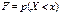 | 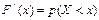 | 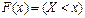 | 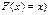 | |||
| 97. | Плотностью распределения НСВ называют функцию: | 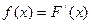 | 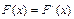 | 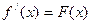 | 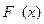 | 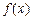 | |||
| 98. | Плотность распределения НСВ обладает свойством: | 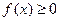 | 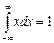 | 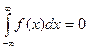 | 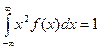 | 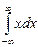 | |||
| 99. | Дисперсия НСВ вычисляется по формуле Д(Х)=: | 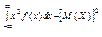 | 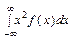 | 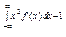 | 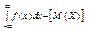 | 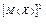 | |||
| 100. | Математическое ожидание постоянной величины (числа) С равно: | С | 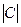 | длина отрезка 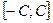 | ln 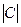 | ||||
| 101. | Дисперсия постоянной величины (числа) С равна: | 0 (ноль) | С  | 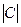 | +  | ln 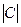 | |||
| 102. | Среднее квадратическое отклонение постоянной величины (числа) С равно: | 0 (ноль) | С | 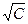 | 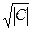 | 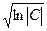 | |||
| 103. | Задан закон распределения дискретной случайной величины Х. Найти математическое ожидание М(Х) 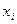 |_23|_25|_28| 29| Р | 0,3|0,2 | 0,4| 0,1| |_23|_25|_28| 29| Р | 0,3|0,2 | 0,4| 0,1| | ||||||||
| 104. | Задан закон распределения дискретной случайной величины Х. Найти дисперсию Д(Х) 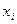 |_23|_25|_28| 29| Р | 0,3|0,2 | 0,4| 0,1| |_23|_25|_28| 29| Р | 0,3|0,2 | 0,4| 0,1| | 5,4 | 0,32 | 2,32 | 2,1 | 0,3 | |||
| 105. | Задан закон распределения дискретной случайной величины Х. Найти среднее квадратическое отклонение 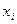 |_23|_25|_28| 29| Р | 0,3|0,2 | 0,4| 0,1| |_23|_25|_28| 29| Р | 0,3|0,2 | 0,4| 0,1| | 2,32 | 0,32 | 23,1 | |||||
| 106. | Плотность распределения непрерывной случайной величины Х в интервале (0; 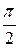 ) равна f(x)=С·sin 3x; вне этого интервала f(x)=0. Найти параметр С. ) равна f(x)=С·sin 3x; вне этого интервала f(x)=0. Найти параметр С. | 2,32 | 0,32 | ||||||
| 107. | Математическое ожидание случайной величины 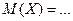 : : | 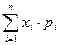 | 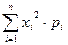 | 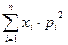 | 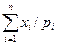 | 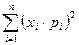 | |||
| 108. | По какой формуле вычисляют математическое ожидание непрерывной случайной величины: | 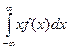 |  pi pi | 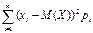 | 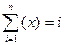 | 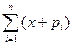 | |||
| 109. | Найти математическое ожидание случайной величины Z, если известны математические ожидания X и Y: Z=X+2Y, M(X)=5, M(Y)=3 | ||||||||
| 110. | Найти математическое ожидание случайной величины Z, если известны математические ожидания X и Y: Z=3X+4Y, M(X)=2, M(Y)=6 | ||||||||
| 111. | Найти дисперсию случайной величины Z, если известны дисперсии X и Y: Z=3X+2Y, Д(X)=5, Д(Y)=6 | ||||||||
| 112. | Найти дисперсию случайной величины Z, если известны дисперсии X и Y: Z=2X+3Y, Д(X)=4, Д(Y)=5 | ||||||||
| 113. | Найти дисперсию случайной величины Х - числа появлений события А в 5 независимых испытаниях, если вероятность появления события А в каждом испытании равна 0,2. | 0,8 | 0,1 | 0,2 | |||||
| 114. | Найти дисперсию случайной величины Х - числа отказов элемента некоторого устройства в 10 независимых опытах, если вероятность отказа элемента в каждом опыте равна 0,9. | 0,9 | 0,1 | ||||||
| 115. | Случайная величина Х задана плотностью распределения f(x)=2x в интервале (0,1); вне этого интервала f(x)=0. Найти математическое ожидание величины Х | 2/3 | 1/3 | 1/2 | |||||
| 116. | Случайная величина Х задана плотностью распределения f(x)=(1/2)x в интервале (0,2); вне этого интервала f(x)=0. Найти математическое ожидание величины Х | 4/3 | 2/3 | 1/3 | 1/2 | ||||
| 117. | Вариационный ряд – это … | Ряд упорядоченный по возрастанию (убыванию) значения количественного признака Х | Ряд количественного признака Х | Часть генеральной | упорядоченный ряд | упорядоченный по возрастанию признак Х | |||
| 118. | Выборка – это… | Часть генеральной совокупности, из которой она извлечена | Часть генерального ряда | Ряд упорядоченный по возрастанию количественного признака | Часть совокупности | извлеченный ряд | |||
| 119. | Размах вариации вычисляют по формуле: | 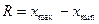 | 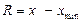 | 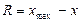 | 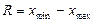 | 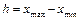 | |||
| 120. | Число групп вычисляют по формуле: | 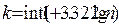 | 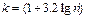 | 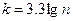 | 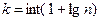 | 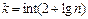 | |||
| 121. | Группировка – это … | Расчленение статистических данных, при котором группы будут содержать качественно однородные элементы | Расчленение статистических данных | статистические данные | группы статистических данных | содержание групп | |||
| 122. | Дискретный признак - | Значения отличаются друг от друга на некоторую конечную величину | Значения признака отличаются друг от друга на сколь угодно малую величину | Значения признака не отличаются друг от друга | Расчленение статистических данных | конечная величина | |||
| 123. | Непрерывный признак- | Значения признака отличаются друг от друга на сколь угодно малую величину | Значения отличаются друг от друга на некоторую конечную величину | Значения признака не отличаются друг от друга | Расчленение статистических данных | конечная величина | |||
| 124. | Шаг группировки вычисляют по формуле: | 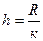 | 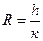 | 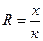 | 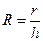 | 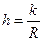 | |||
| 125. | Накопленная частота – это | Суммирование всех частот вариантов, предшествующих данному с частотой этого варианта | Суммирование всех вариантов | произведение всех частот вариантов | разность всех частот вариантов | Суммирование вариантов с частотой варианта | |||
| 126. | Средняя арифметическая простая вычисляется по формуле: | 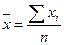 | 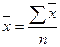 | 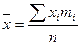 | 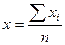 | 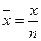 | |||
| 127. | Средняя арифметическая взвешенная вычисляется по формуле: | 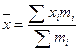 | 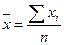 | 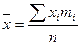 | 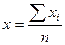 | 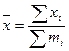 | |||
| 128. | Среднее линейное отклонение простое вычисляется по формуле: | 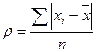 | 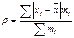 | 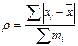 | 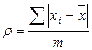 | 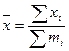 | |||
| 129. | Среднее линейное отклонение взвешенное вычисляется по формуле: | 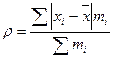 | 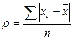 | 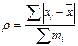 | 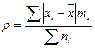 | 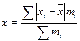 | |||
| 130. | Взвешенная дисперсия вычисляется по формуле: | 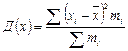 | 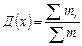 | 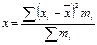 | 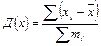 | 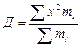 | |||
| 131. | Среднее квадратическое отклонение простое вычисляется по формуле: | 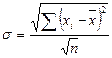 | 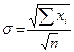 | 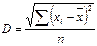 | 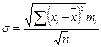 | 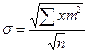 | |||
| 132. | Среднее квадратическое отклонение взвешенное вычисляется по формуле: | 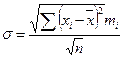 | 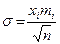 | 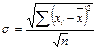 | 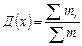 | 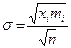 | |||
| 133. | Коэффициент вариации вычисляется по формуле: | 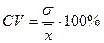 | 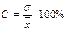 | 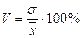 | 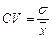 | 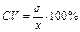 | |||
| 134. | Модой называется: | Такое значение количественного признака которое наблюдалось наибольшее число раз | Значение признака, приходящееся на середину ранжированного ряда | Вариант, которому соответствует наибольшая частота | Такое значение количественного признака которое наблюдалось наименьшее число раз | Значение признака, приходящееся на начало ранжированного ряда | |||
| 135. | Для дискретного вариационного ряда модой является: | Вариант, которому соответствует наибольшая частота | Значение признака, приходящееся на середину ранжированного ряда | Такое значение количественного признака которое наблюдалось наибольшее число раз | Такое значение количественного признака которое наблюдалось наименьшее число раз | Вариант, которому соответствует наименьшая частота | |||
| 136. | Медианой называется: | Значение признака, приходящееся на середину ранжированного ряда | Вариант, которому соответствует наибольшая частота | Такое значение количественного признака которое наблюдалось наибольшее число раз | Значение признака, приходящееся на конец ранжированного ряда | Значение признака, приходящееся на начало ранжированного ряда | |||
| 137. | Если произведено четное число наблюдений, то медиана вычисляется по формуле: | 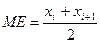 | 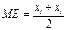 | 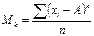 | 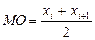 | 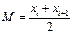 | |||
| 138. | Моменты вариационного ряда относительно числа А вычисляются по формуле: | 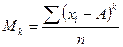 | 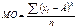 | 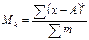 | 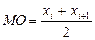 | 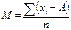 | |||
| 139. | Коэффициент асимметрии вычисляется по формуле: | 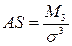 | 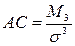 | 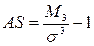 | 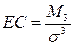 | 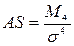 | |||
| 140. | Эксцесс (коэффициент крутизны) вычисляется по формуле: | 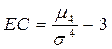 | 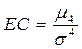 | 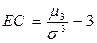 | 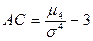 | 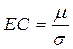 | |||
| 141. | Обычная нормальная кривая Гаусса, если: | 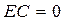 | EC > 0 | EC < 0 | 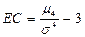 | 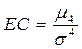 | |||
| 142. | Кривая Гаусса островершинная (крутая), если: | EC > 0 | EC < 0 | 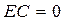 | 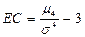 | 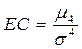 | |||
| 143. | Кривая Гаусса более плоская, если: | EC < 0 | EC > 0 | 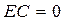 | 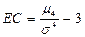 |
Подборка статей по вашей теме:
|
 2015-06-10
2015-06-10 1770
1770