2015-06-10
526
Пусть задано множество, содержащее конечное число элементов. (Студенты в группе, яблоки в корзине, набор костей домино и т.д.) Такие множества будем называть конечными и обозначать {a,b,c,d}. Если каждому элементу конечного множества поставлены в соответствие натуральные числа, то такое упорядоченное множество называется перестановкой и обозначается (a,b,c,d). Сколько перестановок можно составить из n-элементного множества? Из трехэлементного 6: (a,b,c), (a,c,b), (b,a,c), (b,c,a), (c,a,b), (c,b,a).
Число перестановок из n-элементного множества вычисляется по формуле: Рn = n!, где n! - произведение n(n - 1)(n - 2)(n - 3)…3*2*1. Полезна рекуррентная формула Pn = n*Pn-1. Прост и комбинаторный смысл числа перестановок: сколькими способами можно упорядочить конечное n-элементное множество.
Размещением из n по k называется упорядоченное k-элементное подмножество n-элементного множества. По смыслу определения ясно, что k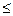 
n. Число размещений из n по k обозначается 
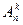. Очевидно, что 
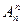= Рn 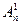= n!, 
= n,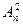 
=n*(n – 1), 
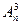=n*(n –1)*(n–2) 
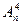=n*(n – 1)*(n – 2)*(n – 3) и т.д. 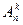-это произведение k старших сомножителя натурального числа n, т. е. 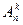= n*(n – 1)*(n – 2)*…*(n – k + 1) (*). Помножая и деля это выражение на (n – k)! можно получить еще формулу:
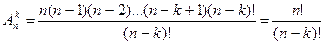= n(n –1)(n – 2)(n –3)…3*2*1, т.е. k старших сомножителя числа n.
Сочетанием из n по k называется неупорядоченное k-элементное подмножество n-элементного множества. По смыслу определения ясно, что k 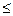n. Число сочетаний из n по k обозначается 
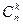. Очевидно, что неупорядоченных подмножеств n-элементного множества в k! меньше чем упорядоченных подмножеств, т.е. = 
(*)
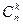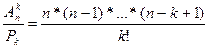Помножая и деля это выражение на (n – k)! можно получить еще формулу:
;
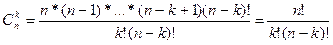На практике, для вычисления 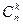используют формулу (*)
Некоторые важные свойства числа сочетаний, которые необходимо применять при решении различных задач:
1) 
= 
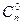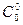= 1; 2) 
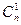= n; 3) = 
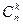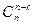-эту формулу удобно применять при k > n/2
4) + + 
+ 
+ … + 
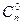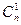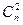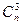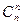= 2n; 5) + 
= 
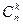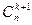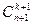-рекуррентная формула.
