Под декомпозицией в общем случае будем понимать представление абстрактного автомата совокупностью нескольких более простых автоматов. В простейшем случае будем рассматривать декомпозицию на параллельно, последовательно или смешанно работающие автоматы. В общем случае это, конечно, не всегда возможно.
Задачу декомпозиции абстрактного автомата можно форму-лировать как задачу разложения автомата по алгебрагическим операциям. Поэтому важно изучение свойств формальных операций над абстрактными автоматами. Рассмотрим задание алгебрагических операций умножения, суммирования автоматов.
Операция умножения автоматов 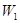 и
и 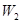 содержательно соответствует параллельной работе автоматов
содержательно соответствует параллельной работе автоматов 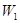 и
и 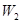 (рис. 7.11). Отсюда следует, что входной сигнал
(рис. 7.11). Отсюда следует, что входной сигнал 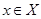 соответствует паре
соответствует паре 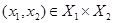 и то же можно сказать о выходном сигнале.
и то же можно сказать о выходном сигнале.
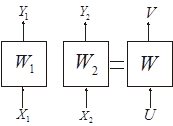
Рис. 7.11. Иллюстрация операции умножения
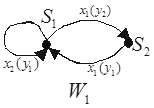
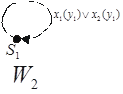
Рис. 7.12. Графы автоматов 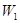 и
и 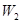
Различают два типа умножения. Первый, обозначаемый 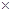 , применяется для автоматов, у которых
, применяется для автоматов, у которых 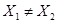 . Второй тип, обозначаемый
. Второй тип, обозначаемый 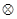 , соответствует случаю
, соответствует случаю 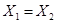 .
.
Пусть автоматы 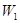 и
и 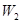 заданы графами на рис. 7.12, причем оба они инициальные с начальными состояниями
заданы графами на рис. 7.12, причем оба они инициальные с начальными состояниями 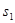 (для
(для 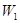 ) и
) и 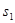 (для
(для 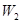 ) или для автомата
) или для автомата 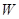 это состояние задается парой
это состояние задается парой 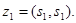 Если приходит сигнал
Если приходит сигнал 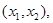 то параллельная работа автомата приводит к состоянию (см. рис. 7.12) (
то параллельная работа автомата приводит к состоянию (см. рис. 7.12) (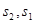 ) с выходным сигналом (
) с выходным сигналом (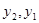 ). Если проанализировать все комбинации выходов и состояний, то получим граф автомата на рис. 7.13.
). Если проанализировать все комбинации выходов и состояний, то получим граф автомата на рис. 7.13.
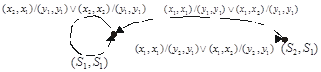
Рис. 7.13. Граф автомата 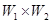
Если теперь ввести алфавиты для полученного автомата 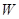 , получим:
, получим:
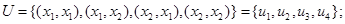
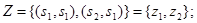
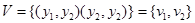
Теперь граф автомата принимает вид как на рис. 7.14.

Рис. 7.14. Модифицированный граф автомата 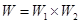
Вторая операция умножения 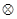 соответствует параллельной работе автоматов
соответствует параллельной работе автоматов 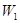 и
и 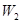 с одним выходом (рис. 7.15).
с одним выходом (рис. 7.15).
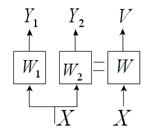
Рис. 7.15. Иллюстрация операции умножения 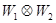
Для примера воспользуемся графами автоматов 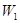 и
и 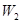 (рис. 7.12) и составим алфавит составного автомата:
(рис. 7.12) и составим алфавит составного автомата:
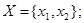
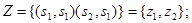
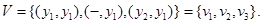
Тогда, полагая, что автоматы 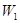 и
и 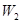 инициальные с начальными состояниями
инициальные с начальными состояниями 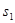 и
и 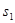 , получим граф автомата
, получим граф автомата 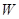 (рис. 7.16).
(рис. 7.16).
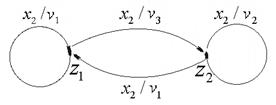
Рис. 7.16. Граф автомата 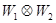
Операция суммирования автоматов 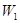 и
и 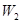 соответствует автомату
соответствует автомату 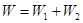 с параллельной неодновременной работой автоматов
с параллельной неодновременной работой автоматов 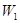 и
и 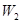 , когда любое входное слово для автомата
, когда любое входное слово для автомата 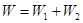 образуется чередованием входных букв автоматов
образуется чередованием входных букв автоматов 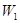 и
и 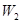 . Точно так же выходное слово для автомата
. Точно так же выходное слово для автомата 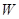 - это чередование выходных слов
- это чередование выходных слов 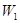 и
и 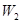 . В этом случае выходное слово можно представить последовательностью
. В этом случае выходное слово можно представить последовательностью 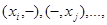 где прочерк означает отсутствие входного сигнала на соответствующий автомат. Последовательность такой же структуры будет и на выходе автомата
где прочерк означает отсутствие входного сигнала на соответствующий автомат. Последовательность такой же структуры будет и на выходе автомата 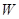 .
.
Для рассматриваемой операции для автоматов 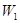 и
и 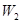 из рис. 7.12 можно получить граф переходов, представленный на рис. 7.17, где обозначения:
из рис. 7.12 можно получить граф переходов, представленный на рис. 7.17, где обозначения: 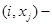 входной сигнал
входной сигнал 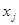 на автомате
на автомате 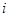 , а
, а 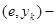 выходной сигнал
выходной сигнал 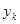 на автомате
на автомате 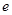 .
.
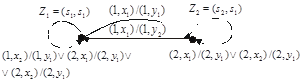
Рис. 7.17. Граф переходов автомата 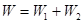
Рассмотрим суперпозицию автоматов 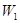 и
и 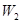 . Эта операция, обозначаемая
. Эта операция, обозначаемая 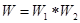 , соответствует последовательной работе автоматов
, соответствует последовательной работе автоматов 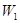 и
и 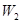 (рис. 7.18).
(рис. 7.18).
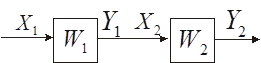
Рис. 7.18. Модель суперпозиции автоматов 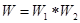
Если автоматы 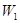 и
и 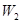 заданы графами переходов, как на рис 7.19, то для суперпозиции
заданы графами переходов, как на рис 7.19, то для суперпозиции 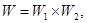 в которой каждый автомат является инициальным с состояниями
в которой каждый автомат является инициальным с состояниями 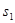 и
и 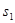 соответственно, граф переходов по состояниям
соответственно, граф переходов по состояниям 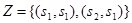 можно изобразить как на рис. 7.20, где
можно изобразить как на рис. 7.20, где 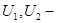 это выходы автомата
это выходы автомата 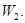
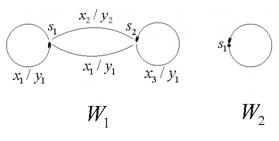
Рис. 7.19. Графы переходов для исходных автоматов 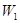 и
и 
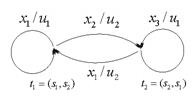
Рис. 7.20. Граф переходов для суперпозиции автоматов
В случае разложения автомата по операции типа 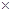 , его декомпозиция называется параллельной декомпозицией на автоматы с различными входными каналами. Если разложение производится по операции
, его декомпозиция называется параллельной декомпозицией на автоматы с различными входными каналами. Если разложение производится по операции 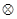 , то это называется параллельной декомпозицией на автоматы с общим входом. Разложению по операции + соответствует параллельная поочередная декомпозиция, а разложение по операции
, то это называется параллельной декомпозицией на автоматы с общим входом. Разложению по операции + соответствует параллельная поочередная декомпозиция, а разложение по операции 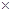 - последовательной декомпозицией.
- последовательной декомпозицией.
Поскольку при задании любой из операций над автоматами 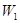 и
и 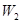 , заданных в матричном виде матрица соединений результирующего автомата
, заданных в матричном виде матрица соединений результирующего автомата 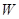 имеет определенную структуру, то для установления возможности декомпозиции некоторого автомата, анализируют его матрицу соединений, используя специальные алгоритмы на принадлежность той или иной конфигурации.
имеет определенную структуру, то для установления возможности декомпозиции некоторого автомата, анализируют его матрицу соединений, используя специальные алгоритмы на принадлежность той или иной конфигурации.
 2015-06-10
2015-06-10 1083
1083








