Пример 3. 2 события

События. Операции над событиями

Одним из основных понятий теории вероятностей является понятие события. «Случайное событие» (или просто «событие») следует рассматривать как исходное неопределяемое понятие теории вероятностей, как, например, понятия точки и прямой в евклидовой геометрии. Поясним его смысл.

Пример 3.1

Рассмотрим опыт (испытание), заключающийся в подбрасывании игральной кости (кубика с шестью гранями). Обозначим через 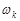выпадение 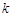очков на верхней грани. Тогда событие - «выпадение четного числа очков» можно представить как множество .

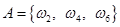Пример 3.2

Пусть в том же испытании нас интересует событие «выпадение 5 очков». Соответствующее множество .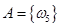

Итак, событие — это некоторое множество возможных исходов испытания. Математической моделью события в теории вероятностей является множество. Если это множество содержит один элемент, как в примере 3.2, то событие (исход) называется элементарным.

Множество 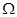всех элементарных исходов испытания называется пространством элементарных событий данного испытания. В примере 3.1 .

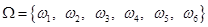Очевидно, событие всегда является некоторым подмножеством пространства элементарных событий: 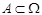(пример 3.1).

Если 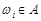, то говорят, что элементарный исход 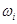благоприятствует событию А. Так в примере 3.1 событию 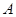«выпало четное число очков» благоприятствуют элементарные исходы 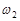, 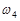и .

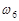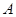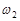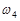Это означает, что событие совершается, если наступает хотя бы один из исходов или , или .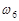

Итак, с каждым испытанием связано некоторое множество 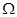– пространство элементарных событий этого испытания.

Очевидно, выбор пространства элементарных событий в каждом случае должен сообразовываться со смыслом конкретного испытания. Так, при подбрасывании игральной кости напрашивается «естественный» выбор пространства элементарных событий: 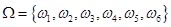. Но, допустим, игра заключается в ставках на «чет» — «нечет». Тогда нет нужды различать исходы 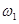, , 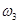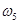так же, как и исходы 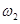, , 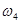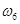. В этом случае события 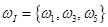и 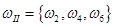следует считать элементар­ными, и пространство элементарных событий имеет вид .

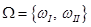Множество 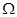, как и всякое множество, связанное с испы­танием, является событием. Оно наступает при любом исходе испытания, так как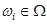 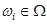при всех 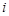. Поэтому множество 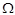называют достоверным событием. Обычно достоверное собы­тие обозначается U. Таким образом, 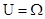. Пустое множест­во 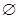интерпретируется как невозможное событие. В реаль­ной ситуации это событие, которое никогда не наступает в данном испытании. Невозможное событие обычно обознача­ется V, т. е. V = .

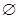Операции над событиями – сумма, произведение и раз­ность – определяются как соответствующие операции над множествами.

Пусть 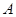и 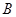являются подмножествами пространства ,

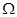т. е. событиями, которые могут произойти в результате одно­го и того же испытания.

Суммой (или объединением) событи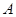й и 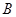будет событие 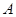+ 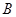(или 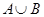), элементарные исходы которого благоприятствуют хотя бы одному из событий 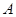или В. В ре­альном испытании это означает, что происходит, по крайней мере, одно из событий А или В (возможно, имеют место оба события).

Произведением (или пересечением) событи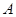й и 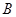называется событие АВ (или 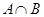), элементарные исходы которого благопри­ятствуют и 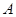и В. В реальном испытании событие АВ заключается в том, что имеют место и событие 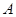и собы­тие В.

Разностью событий 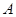и 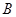называется событие 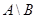, элементы которого благоприятствуют событию 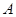, но не бла­гоприятствуют 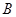. В реальном испытании событие 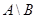заключается в том, что 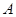произошло, а 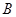не произошло. На рис. 3.1 приведены соответствующие диаграммы Эйлера-Венна.

а б в

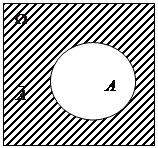Рис 3.1

Рис. 3.2

Событие 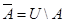называется противоположным событию 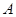(рис.3.2). Появление события 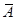в испытании исключает возможность осуществления события А. Очевидно, , .

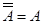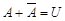События 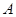и 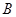называются несовместными, если 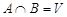(или то же самое можно записать ).

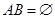Очевидно, противоположные события несовместны: 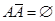, (или тоже самое можно записать так ).

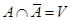С помощью введенных операции из некоторых заданных событий можно конструировать сложные события.