2015-06-10
308
Студент, из 30 билетов выучил первые 20. На экзамен он пришел одним из последних, когда осталось только 8 билетов с 17-го по 24-й (событие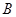 
= {17, 18, 19, 20, 21, 22, 23, 24}). Обозначим A = {студенту достался знакомый билет}.
Если, придя на экзамен, студент не получил никакой информации об оставшихся билетах, то по классическому определению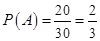 
. Если же он узнал, что событие 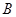произошло, то для него вероятность получить выученный, билет изменится. Общее число возможных исходов теперь – это число оставшихся билетов – 8. Благоприятствующие исходы {17, 18, 19, 20}, их число – 4. Вероятность события A при условии, что имело место событие B («условная вероятность») 
=
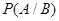= 4/8 =1/2.
Можно показать, что для классического испытания с равновозможными исходами имеет место формула
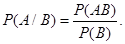
| (3.6) |
Формула (3.6) принимается за определение условной вероятности и в общем случае.
Можно показать, что величина 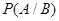, определенная формулой (3.6) удовлетворяет аксиомам вероятности 1–3, поэтому (3.6) называют четвертой аксиомой вероятности.
