Теоретическое введение

БАРАКИН В.В., РЫБАКОВ А.Г., ВЕСЕЛКОВ А.Н.

ЛАБОРАТОРНАЯ РАБОТА № 19.1

Определение коэффициента теплопроводности воздуха

1. ЦЕЛЬ РАБОТЫ:

1. Изучение основных законов теплопроводности газов.

2. Определение коэффициента теплопроводности воздуха.

2 ЛИТЕРАТУРА:

1. Савельев И.В. Курс общей физики: Учеб. пособие для студентов втузов.-2-е изд., перераб. - М.: Наука, 1982. -Т.1.: Механика.-432 с.

2. Матвеев А.Н. Молекулярная физика: Учеб. пособие для вузов.- М.: Высшая школа, 1981. - 400 с., ил.

3. Сивухин Д.В. Термодинамика и молекулярная физика: Учеб. пособие для вузов.- 3-е изд., испр. и доп. - М.: Гл. ред. физ.-мат. лит., 1990.- 592 с. - (Общий курс физики; Т. 2).

ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

Рассмотрим процесс теплопроводности в газах (рис.1).

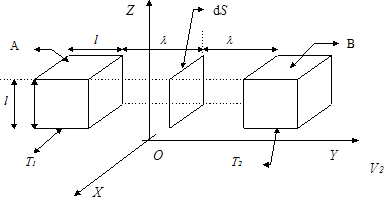
Рис. 1

Пусть изменение температуры происходит в направлении оси перпендикулярно площадке и . Тогда количества тепла 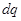, переносимое через перпендикулярную площадку 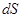, пропорционально величине площадки 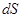, промежутку времени 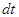, за который наблюдается рассмотренный перенос тепла и градиенту температуры 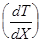, т.е:

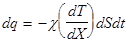, (1)

где 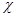- коэффициент теплопроводности, который зависит от газа и условий, при которых он находится.

Знак минус в соотношении (1) указывает на то, что перенос тепла происходит в направлении уменьшении температуры, т.е. в сторону оси .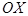

Рассмотрим металлический цилиндр радиуса 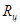, в котором находится исследуемый газ и вдоль оси которого натянута металлическая проволока AB (рис. 2).

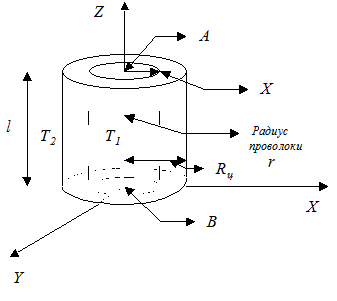
Рис. 2

Если проволоку AB нагревать током, то при стационарных условиях в направлении радиуса трубки возникает определенный градиент температуры и в этом же направлении наблюдается перенос тепловой энергии. При этом количество тепла, переносимое через боковую поверхность коаксиального цилиндра радиуса 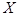можно определить по формуле:

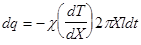, (2)

где 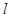- длина проволоки (цилиндра).

При установившемся процессе количество теплоты, переносимой через рассматриваемую поверхность в единицу времени будет величиной постоянной. Таким образом:

.

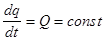Следовательно, соотношение (2) будет иметь следующий вид:

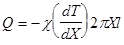. (3)

Решим дифференциальное уравнение (3) методом разделения переменных. Для этого соотношение (3) перепишем в следующем виде:

.

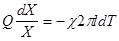Проинтегрировав последнее уравнение,

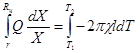, получим:

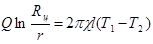. (4)

Из уравнения (4) можно определить коэффициент теплопроводности 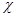исследуемого газа:

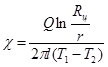, (5)

где: 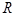- радиус цилиндра; 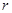- радиус проволоки; 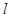- длина цилиндра (проволоки); 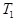- температура проволоки; 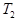- температура цилиндра.

Таким образом, для определения коэффициента теплопроводности исследуемого газа необходимо найти количество тепловой энергии, передаваемой от проволоки к стенки цилиндра путем теплопроводности.

Это количество теплоты можно определить по закону Джоуля - Ленца

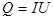, (6)

где 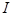- ток, протекающий по проволоке; 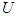- падение напряжения на проволоке.

Следует, однако, учитывать, что рассчитанное при этом значение теплопроводности будет иметь несколько завышенное значение, так как помимо теплопроводности передача тепла может осуществляться излучением, за счет конвекции и в результате передачи тепла от проволоки через электрические контакты к подводящим проводам.

При выполнении данной работы и при соответствующих расчетах коэффициента теплопроводности процессами конвекции и теплопроводности через подводящие провода мы будем пренебрегать. Что касается теплового излучения, то в данной лабораторной работе количество тепла, передаваемое разогретой проволокой можно оценить с использованием закона Стефана - Больцмана. В соответствии с этим законом энергетическая светимость абсолютно черного тела прямо пропорциональна четвертой степени абсолютной температуры:

,

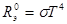где 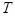- температура абсолютно черного тела; 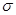- постоянная Стефана - Больцмана, 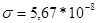(Дж/(м²К⁴с)).

В настоящей работе проволока не является абсолютно черным телом, поэтому закон Стефана - Больцмана будет иметь следующий вид:

,

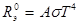где 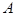- поглощательная способность тела (проволоки).

Для стальной проволоки, используемой в работе 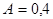. Если - площадь нагретой проволоки, 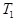- её температура, 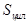-площадь боковой поверхности цилиндра, 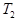- температура стенки цилиндра, то тепловая энергия 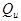, передаваемая от проволоки к цилиндру через излучение в единицу времени, равна:

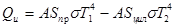. (7)

Расчеты по формуле (7) показывают, что количество теплоты 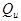, передаваемое проволокой через излучение в единицу времени составляет несколько процентов от энергии, выделяемой текущим по проволоке током согласно соотношению (6), и в данной работе не учитываются.

Так как мощность, выделяемая при протекании тока, определяется соотношением (6), то, подставляя соотношение (6) в уравнение (5), получим рабочую формулу для расчета коэффициента теплопроводности воздуха.

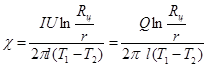. (8)