Теория вероятностей — раздел математики, изучающий закономерности случайных явлений.
Опытом называется воспроизводимый комплекс условий, при которых наблюдается изучаемое случайное явление. Пример. Подбрасывание игральной кости или монеты.
Событие — это любая качественная или количественная характеристика изучаемого случайного явления. Событие называется достоверным, если оно всегда наступает в результате опыта. Событие называется невозможным, если оно не может наступить в результате опыта.
В случае с подбрасыванием монеты случайными событиями будут являться «орел» или «решка». В случае игральной кости случайные события могут быть более разнообразными, например: появление на верхней грани игральной кости единицы; числа, большего трех; простого числа и т. д.
Случайные события будем обозначать большими латинскими буквами A, B и т.д.
Невозможное событие будем обозначать буквой V, а достоверное буквой U.
Определение (классическое определение вероятности):
Вероятностью события A называется число P(A)=m/n, где n -число всевозможных, взаимоисключающих и равновозможных исходов рассматриваемого опыта, m -число тех из них, которые благоприятны событию A.
Из определения вероятностей следует, что вероятность любого события не меньше нуля и не больше единицы: 0≤P(A)≤1, кроме того P(V)=0, а P(U)=1.
Пример. Опыт заключается в бросании мяча в баскетбольное кольцо. В результате проведения опыта возможно два исхода: «мяч в кольце» или «промах». Студент Петров 10 раз бросал мяч в кольцо, из них промахов было семь, а попаданий - три. Таким образом, в данной серии бросков вероятность события "мяч в кольце" равна 0,3, а вероятность "промаха" - 0,7.
Определение. Суммой событий A и B называется событие C, заключающееся в том, что произошло хотя бы одно из двух событий A или B. Тот факт, что событие C является суммой событий A и B записывают так: C=A+B или 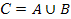 .
.
Определение. Произведением событий A и B называется событие C, заключающееся в том, что произошли оба события A и B. Тот факт, что событие C является произведением событий A и B записывают так: C=A∗B или 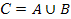 .
.
Определение. Событием, противоположным событию A, называется событие 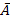 , заключающееся в том, что событие A не произошло.
, заключающееся в том, что событие A не произошло.
Задача 1. В ящике 5 апельсинов и 4 яблока. Наудачу выбираются 3 фрукта. Какова вероятность, что все три фрукта – апельсины?
Решение. Элементарными исходами здесь являются наборы, включающие 3 фрукта. Поскольку порядок фруктов безразличен, будем считать их выбор неупорядоченным (и бесповторным). Общее число элементарных исходов 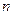 равно числу способов выбрать 3 фрукта из 9, т.е. числу сочетаний
равно числу способов выбрать 3 фрукта из 9, т.е. числу сочетаний 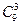 . Число благоприятствующих исходов
. Число благоприятствующих исходов 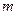 равно числу способов выбора 3 апельсинов из имеющихся 5, т.е.
равно числу способов выбора 3 апельсинов из имеющихся 5, т.е. 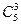 . Тогда искомая вероятность
. Тогда искомая вероятность
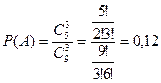 .
.
Задача 2. Преподаватель предлагает каждому из трех студентов задумать любое число от 1 до 10. Считая, что выбор каждым из студентов любого числа из заданных равновозможен, найти вероятность того, что у кого-то из них задуманные числа совпадут.
Решение. Подсчитаем общее количество исходов. Первый из студентов выбирает одно из 10 чисел и имеет n1=10 возможностей, второй тоже имеет n2=10 возможностей, наконец, третий также имеет n3=10 возможностей. В силу правила умножения общее число способов равно: n= n1´n2´n3=103 = 1000, т.е. все пространство содержит 1000 элементарных исходов.
Для вычисления вероятности события A удобно перейти к противоположному событию, т.е. подсчитать количество тех случаев, когда все три студента задумывают разные числа. Первый из них по-прежнему имеет m1=10 способов выбора числа. Второй студент имеет теперь лишь m2=9 возможностей, поскольку ему приходится заботиться о том, чтобы его число не совпало с задуманным числом первого студента. Третий студент еще более ограничен в выборе — у него всего m3=8 возможностей. Поэтому общее число комбинаций задуманных чисел, в которых нет совпадений, равно m=10×9×8=720. Случаев, в которых есть совпадения, остается 280. Следовательно, искомая вероятность равна Р=280/1000= 0,28.
Задача 3. Пусть в урне имеется N шаров, из них М белых и N–M черных. Из урны извлекается n шаров. Найти вероятность того, что среди них окажется ровно m белых шаров.
Решение. Так как порядок элементов здесь несущественен, то число всех возможных наборов объема n из N элементов равно числу сочетаний 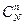 . Число испытаний, которые благоприятcтвуют событию А – "m белых шаров, n–m черных", равно
. Число испытаний, которые благоприятcтвуют событию А – "m белых шаров, n–m черных", равно 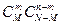 , и, следовательно, искомая вероятность равна Р(А)=
, и, следовательно, искомая вероятность равна Р(А)= 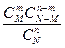 .
.
Задача 4. Точку наудачу бросили на отрезок [0; 2]. Какова вероятность ее попадания в отрезок [0,5; 1,4]?
Решение. Здесь пространство элементарных исходов весь отрезок 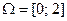 , а множество благоприятствующих исходов
, а множество благоприятствующих исходов 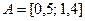 , при этом длины этих отрезков равны
, при этом длины этих отрезков равны 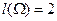 и
и 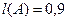 соответственно. Поэтому
соответственно. Поэтому
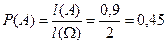 .
.
Задача 5(задача о встрече). Два лица А и В условились встретиться в определенном месте между 12 и 13 часами. Пришедший первым ждет другого в течении 20 минут, после чего уходит. Чему равна вероятность встречи лиц А и В, если приход каждого из них может произойти наудачу в течении указанного часа и моменты прихода независимы?
Решение. Обозначим момент прихода лица А через х и лица В – через у. Для того, чтобы встреча произошла, необходимо и достаточно, чтобы ôх-уô£20. Изобразим х и у как координаты на плоскости, в качестве единицы масштаба выберем минуту. Всевозможные исходы представляются точками квадрата со стороной 60, а благоприятствующие встрече располагаются в заштрихованной области. Искомая вероятность равна отношению площади заштрихованной фигуры (рис. 2.1) к площади всего квадрата: P(A) = (602–402)/602 = 5/9.
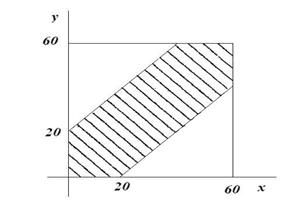
Рис. 2.1.
 2015-06-10
2015-06-10 3733
3733