Частотный метод В.М. Попова

Частотный метод В.М. Попова решает задачу об абсолютной устойчивости системы с одной однозначной нелинейностью, заданной предельным значением коэффициента передачи k нелинейного элемента.

Если в системе управления (рис. 2.5) имеется лишь одна однозначная нелинейность

y_н = F(x), (2.11)

то, объединив вместе все остальные звенья системы в линейную часть, можно получить ее передаточную функцию W_лч(s).

Нелинейность y_н = F(x) имеет любое очертание, не выходящее за пределы заданного угла arctg k (рис. 2.7), т.е. при любом x

0 £ F(x) £ kx. (2.12)

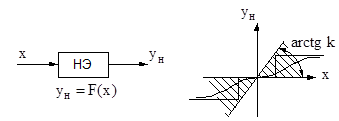
а) б)

Рис. 2.7. Нелинейность системы:

а) нелинейный элемент; б) статические характеристики

Теорема В.М. Попова [2]: для установления абсолютной устойчивости нелинейной системы достаточно подобрать такое конечное действительное число q, при котором для всех частот w ³ 0

Re[(1+ jwq)W_ЛЧ(jw)] + 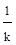> 0, (2.13)

где k - предельное значение коэффициента передачи нелинейного элемента;

W_ЛЧ(jw) - амплитудно-фазовая частотная характеристика линейной части системы.

Все полюсы передаточной функции линейной части системы должны быть с отрицательными вещественными частями или же кроме них имеется еще не более двух нулевых. При наличии одного нулевого полюса требуется еще, чтобы

Im W_ЛЧ(jw) ® -¥ при w ® 0,

а при двух нулевых полюсах

Re W_ЛЧ(jw) ® -¥ при w ® 0, а Im W_ЛЧ(jw) < 0 при малых w.

Другая формулировка той же теоремы, дающая удобную графическую интерпретацию, связана с введением видоизмененной частотной характеристики линейной части системы W*(jw), которая определяется следующим образом:

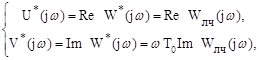(2.14)

где T₀= 1 с - нормирующий множитель.

Преобразовав левую часть неравенства (2.13)

Re[(1+ jwq)W_ЛЧ(jw)] + 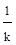= Re W_ЛЧ(jw) - wq Im W_ЛЧ(jw)] +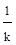

и использовав соотношения (2.14), получим вместо (2.13) для теоремы В.М. Попова условие

U^*(w) - 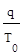V^*(w) + 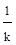> 0 (2.15)

при всех w ³ 0.

Очевидно, что равенство

U^*(w) - 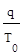V^*(w) + 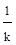= 0 (2.16)

представляет собой уравнение прямой на плоскости W^*(jw). Эта прямая, называемая прямой Попова, проходит через точку с координатами [-1/k, j0] и имеет угловой коэффициент наклона к оси абсцисс 1/q.

Отсюда вытекает графическая интерпретация теоремы В.М.Попова [2]: для установления абсолютной устойчивости нелинейной системы достаточно подобрать такую прямую на комплексной плоскости W^*(jw), проходящую через точку (- 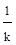, j0), чтобы вся кривая W^*(jw) лежала справа от этой прямой.

Условия выполнения теоремы. показаны на рис. 2.8.

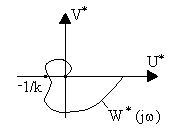
а) б)

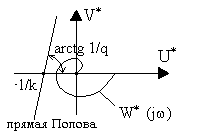
Рис. 2.8. Графическая интерпретация теоремы В.М. Попова:

а - абсолютно устойчивая система; б - система не имеет абсолютной устойчивости

На рис. 2.8,а приведен случай абсолютной устойчивости нелинейной системы при любой форме однозначной нелинейности, ограниченной лишь условием (2.12), а рис. 2.8,б соответствует случаю невыполнения теоремы, т.е. нелинейная система не имеет абсолютной устойчивости.

Таким образом, для определения абсолютной устойчивости нелинейной системы по методу В.М. Попова необходимо построить видоизмененную частотную характеристику линейной части системы W^*(jw), определить предельное значение коэффициента передачи k нелинейного элемента из условия 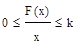и через точку (- 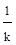) на вещественной оси комплексной плоскости провести некоторую прямую так, чтобы характеристика W^*(jw) лежала справа от этой прямой. Если такую прямую провести нельзя, то это значит, что абсолютная устойчивость для данной системы невозможна. Величина q, связанная с угловым коэффициентом, при этом определяется из условия (2.15) так, чтобы при известных параметрах системы неравенство соблюдалось для всех частот. Очертание нелинейности может быть неизвестным. Необходимо знать лишь, в пределах какого угла arctg k (рис. 2.7,б) она расположена. Для конкретно заданных форм нелинейности область устойчивости будет несколько шире, но данным методом это не определяется.

Дополнение: неравенство (2.13) является так же достаточным условием абсолютной устойчивости нелинейной системы и при k ® ¥.

Пример. Определить предельное значение коэффициента передачи k нелинейного элемента из условия обеспечения абсолютной устойчивости нелинейной системы, передаточная функция линейной части которой

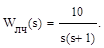
Р е ш е н и е. По передаточной функции линейной части системы находим ее частотную передаточную функцию

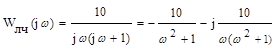откуда получаем видоизмененную частотную характеристику

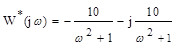
и строим ее на комплексной плоскости, изменяя частоту w от 0 до ¥ (рис. 2.9).

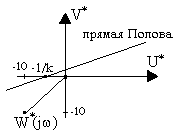
Рис. 2.9. Видоизмененная частотная характеристика

Как видно из последнего выражения, видоизмененная частотная характеристика W^*(jw) представляет собой отрезок прямой линии между точками с координатами [-10, -j10] и [0, -j0].

Следовательно, прямая Попова может быть проведена для любого положительного значения коэффициента передачи k нелинейного элемента так, что вся характеристика W^*(jw) будет лежать справа от этой прямой.

Таким образом, исследуемая нелинейная система абсолютно устойчива при k > 0.