Действительное число, как предел последовательности рациональных чисел

Прежде чем дать определение числовой прямой полезно доказать следующую теорему, которая устанавливает тот факт, что любое действительное число можно представить, как предел последовательности из рациональных чисел.

Теорема 6.1.1. Каждый интервал (a,b) содержит рациональное число.

Доказательство. Пусть h=b-a. По принципу Архимеда найдется такое целое n, что h>1/n. Для числа a, по принципу Архимеда, можно найти такое целое m, что m/n<a<(m+1)/n. Тогда b-a>1/n или b>1/n+a>1/n+m/n=(m+1)/n. Таким образом, a<(m+1)/n<b, ч.т.д.

Следствие. Любое число из R можно представить, как предел последовательности рациональных чисел. Действительно, пусть a произвольное число из R. Рассмотрим интервалы 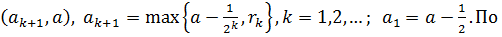теореме 6.1.1 в каждом таком интервале существует рациональное число 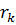. Очевидно, что построенная последовательность монотонно возрастает и ограничена сверху, а значит, имеет предел по теореме Вейерштрасса. Кроме того, по построению, 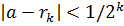. Поэтому 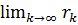= a ч.т.д.