Непрерывные случайные величины.
Множество значений непрерывной случайной величины несчетно и обычно представляет собой некоторый промежуток конечный или бесконечный.
Случайная величина X (w),заданная в вероятностном пространстве {W,S,P}, называется непрерывной (абсолютно непрерывной) W, если существует неотрицательная функция такая, что при любых х функцию распределения FX(x) можно представить в виде интеграла
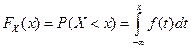 .
.
Функция 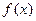 называется функцией плотности распределения вероятностей.
называется функцией плотности распределения вероятностей.
Из определения вытекают свойства функции плотности распределения 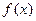 :
:
1. Плотность распределения неотрицательна: 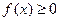 .
.
2. Интеграл по всей числовой прямой от плотности распределения вероятностей равен единице: 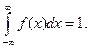
3. В точках непрерывности плотность распределения равна производной функции распределения: 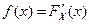 .
.
4. Плотность распределения определяет закон распределения случайной величины, т.к. определяет вероятность попадания случайной величины на интервал 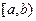 :
:
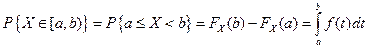 .
.
5.Вероятность того, что непрерывная случайная величина примет конкретное значение 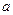 равна нулю:
равна нулю: 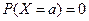 . Поэтому справедливы следующие равенства:
. Поэтому справедливы следующие равенства:
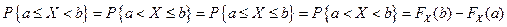 .
.
Задача 1. Функция плотности непрерывной случайной величины имеет вид:
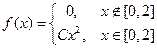
Определить константу C, построить функцию распределения FX(x) и вычислить вероятность 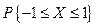 .
.
Решение. Константа C находится из условия 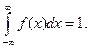 Имеем:
Имеем:
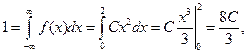 откуда C=3/8.
откуда C=3/8.
Чтобы построить функцию распределения 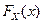 , отметим, что интервал [0,2] делит область значений аргумента x (числовую ось) на три части:
, отметим, что интервал [0,2] делит область значений аргумента x (числовую ось) на три части: 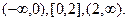 Рассмотрим каждый из этих интервалов. В первом случае (когда x<0) вероятность события {X<x} вычисляется так:
Рассмотрим каждый из этих интервалов. В первом случае (когда x<0) вероятность события {X<x} вычисляется так:
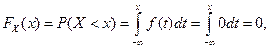
так как плотность X на полуоси 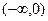 равна нулю. Во втором случае
равна нулю. Во втором случае
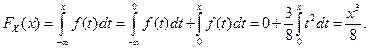
Наконец, в последнем случае, когда x>2,
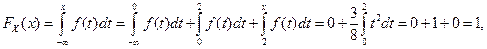 так как плотность
так как плотность 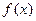 обращается в нуль на полуоси
обращается в нуль на полуоси 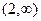 . Итак, получена функция распределения
. Итак, получена функция распределения
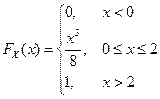
Вероятность 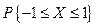 вычислим по формуле
вычислим по формуле 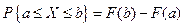 . Таким образом,
. Таким образом, 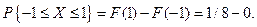
 2015-06-10
2015-06-10 340
340







