2015-06-10
364
Режима работы судна
(Аналитическое решение)
| Вар | |||||||||||
| А | |||||||||||
| С1 | |||||||||||
| С2 | |||||||||||
| C3 | |||||||||||
| K2 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,5 | 1,4 | 1,3 | 1,2 | 1,3 | 1,4 |
| Вар | |||||||||||
| Л | |||||||||||
| С1 | |||||||||||
| С2 | |||||||||||
| С3 | |||||||||||
| K2 | 1,5 | 1,6 | 1,7 | 1,7 | 1,8 | 1,6 | 1,5 | 1,6 | 1,7 | 1,8 | 1,7 |
А - суточная добыча, т
K2 - коэффициент расхода сырья на 1 т. второго вида продукции.
С1,С2,С3 - оптовая цена за 1 т. различного вида продукции.
1. Составить математическую модель задачи выбора оптимального технологического режима траулера по своим данным с учетом возможностей выпуска различных видов продукции в объеме 40, 20 и 2 т. и коэффициентов расхода сырья на выпуск 1 т. Готовой продукции соответственно 1,0 К2, 2,0.
2. Заполнить исходную симплекс-матрицу и выполнить необходимое число итераций для получения оптимального решения.
3. Проанализировать полученное решение с учетом заданных условий и возможных изменений условий (изменение цен, увеличения или уменьшения вылова и т.д.).
4.Составить и решить задачу выбора оптимального режима работы промыслового судна по опыту своей работы, если исполнитель работает судоводителем промыслового судна.
Методика решения задач рассмотрена в конспекте лекций, в [1] стр. 109-131, [2], стр. 16-35, [3], стр. 44-54, [4], стр. 132-136.
II. Выбор управляющих действий в условиях неопределенности
Применение теории игр.
Наиболее простыми являются игры с участием 2-х игроков, имеющих права на два хода или игры два на два (2х2)
В любой игре главным является составление платежной матрицы – это прямоугольная таблица, каждая строка которой представляет собой способ действия одной из сторон, а каждый столбец – действия другой стороны. В пересечении столбцов и строк стоит число, характеризующее платеж, т.е. выигрыш одной из сторон и проигрыш другой.
Возможен лов рыбы в 3-х районах:
Например,
Район А – 8 тралений
В – 6 тралений
С – 5 тралений
Вылов в тоннах на траление при промысловой обстановке или действиях природы:
Район Хороший Улов средний улов плохой улов
А 5 т/тр 3 1
В 6 4 3
С 8 5 2
Матрица добычи при различных действиях рыбака и состояниях природы принимают вид.
Таблица 3
| Природа рыбак | Хороший улов | Средний улов | Плохой улов | Min строк |
| А | ||||
| В | ||||
| С | ||||
| Max столбца |
Существует несколько способов решения задач теории игр.
1-й способ:
Определяем седловую точку матрицы. Если в матрице есть цифра, которая наименьшая в своей строке и наибольшая в своем столбце, то эта клетка и есть седловая точка матрицы. Она является решением игры, т.е. определяет разумные действия обоих противников. Цифровые значения седловой точки есть цена игры (цена игры – это то значение выигрыша одной из сторон и проигрыша другой стороны, которые получат оба игрока при разумных действиях).
2-й способ:
Если в матрице нет седловой точки, то сначала отбрасываются невыгодные или выгодные (доминирующие) одному из противников действия.
При наличии седловой точки, такой способ приведет к этой точке.
Отбрасывание доминирующих стратегий максимально упрощает матрицу.
В таблице 3 приведено решение задачи методом седловой точки. Это решение показывает, что лучшими условиями обеих игроков являются для рыбака район В, для природы – плохие уловы. Цена игры 18 т.
Аналогичное решение получим путем исключения для природы заведомо невыгодной стратегии – хорошие уловы, а потом средние уловы. В оставшемся столбце рыбак, естественно, выберет работу в районе В, поскольку лучше ловить по 18 т,чем 8т или 10 т.
Решение матрицы 2х2, не имеющей седловой точки покажем на примере.
Пример № 2:
Таблица 4
| Природа рыбак | Хороший улов | Средний улов | Плохой улов | Min строк |
| Доп.тр. | ||||
| Кош.н. | ||||
| Пел.тр. | ||||
| Max столб. |
Итоговая матрица 2х2 не имеет седловой точки:
Таблица 5
| Природа Рыбак | Средний улов | Плохой улов |
| Д.тр. | а11=20 | а12=40 |
| П.нев. | а21=70 | а22=30 |
Р1=2/3
Р2=1/3
Чистой стратегии для выигрыша нет, и действия необходимо применять с определенной частотой.
Частоты применения стратегий рассчитывается по формулам.
Задачу выбора смешанных действий или стратегий можно решить также по следующему алгоритму:
v Вычесть числа 1-ой строки из большего меньшее и записать результат напротив второй строки;
v Вычесть во второй строке из большего числа меньшее и результат записать напротив 1-ой строки.
Отношение этих чисел дает частоту применения стратегий рыбака. За природу частоту можно определить, поступив точно также со столбцами.
Графическое решение этой задачи можно выполнить по схеме.
 |
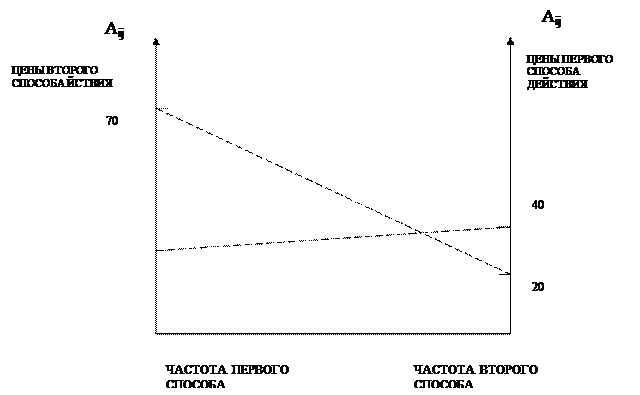Рис. 3. Графическое определение частот.
Цена игры по смешанным стратегиям определяется по следующим формулам:
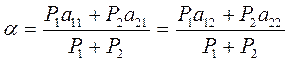- цена игры (2.1.1)
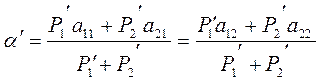(2.1.2)
По нашему примеру:
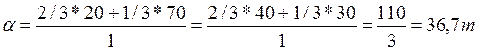
При смешанных стратегиях действия игроков выполняется с заданной частотой случайным образом, используя компьютерное решение случайных чисел с заданной частотой или другой _ метод.
Формула для определения частоты:
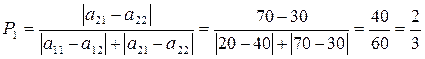(2.1.3)
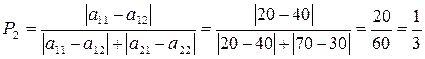(2.1.4)
Полученное методом теории игр решение дает наиболее осторожные действия промысловика при которых он получает min, но гарантированные результаты.
