2015-06-04
2440
Переход от ламинарного к турбулентному режиму течения вызывает увеличение потерь по длине. Это можно объяснить, во-первых, тем, что, перемещаясь от одного сечения потока к другому, любая частица жидкости при ламинарном движении проходит путь, равный расстоянию между этими сечениями. При турбулентном же режиме она помимо участия в общем движении совершает собственные движения, т.е. перемещается по более сложной траектории. В результате проходимый частицей путь значительно превышает расстояние между этими сечениями. Во-вторых, сам характер потерь здесь существенно иной - они определяются уже не трением между слоями, а обменом импульсами между макрочастицами жидкости.
Основной расчётной формулой для определения потерь напора в трубах при турбулентном течении является формула Дарси-Вейсбаха
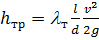, (5.8)
где l т – коэффициент потерь на трение при турбулентном течении.
Коэффициент трения l тв общем случае турбулентного течения жидкости зависит от числа Рейнольдса и от величины относительной шероховатости
|
|
|
,
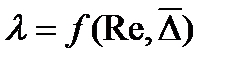где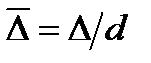 
- относительная шероховатость.
В гидравлически гладкой трубе l т является функцией только числа Re -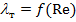 
, так как шероховатость стенок находится под ламинарным слоем потока и не влияет на сопротивление. Для определения этой зависимости существует ряд эмпирических и полуэмпирических формул.
1. Одной из самых распространенных является формула Блазиуса (1912 г.), которая применяется при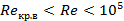 
, имеет следующий вид
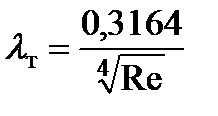. (5.9)
Формула Блазиуса получена экспериментально на основании измерения потерь в латунных трубах при относительно малых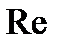 
. Она хорошо согласуется с опытом при числах 
.
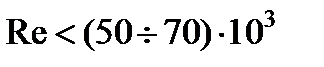Если труба остается гидравлически гладкой до более высоких значений критерия Re, то развитие турбулентного ядра и уменьшение толщины ламинарной пленки приводит к изменению величины степенного коэффициента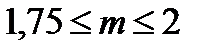 
в формуле (5.10)
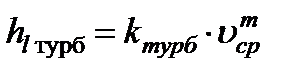, (5.10)
между тем как Блазиус принял его постоянным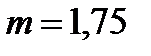 
.
2. Более универсальной оказалась логарифмическая зависимость, предложенная советским физиком Конаковым в 1946 г.
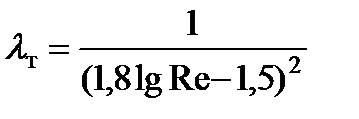. (5.11)
Как подтвердили опыты, эта формула остается справедливой для гидравлически гладких труб в диапазоне
,
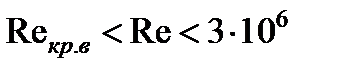т.е. практически всегда, если только выполняется условие
.
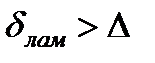Изменение коэффициента трения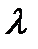 
в интервале чисел 
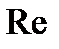, охватывающем ламинарный режим и турбулентное течение в гладких трубах, представлено на рис.5.7.
В области гидравлически гладких труб коэффициент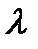 
с увеличением 
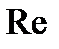, как и при ламинарном режиме, уменьшается, но поболее пологой кривой. Как в том, так и в другом случае падение 
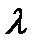вызывается одной и той же причиной - уменьшением роли сил трения по сравнению с инерционными.
|
|
|
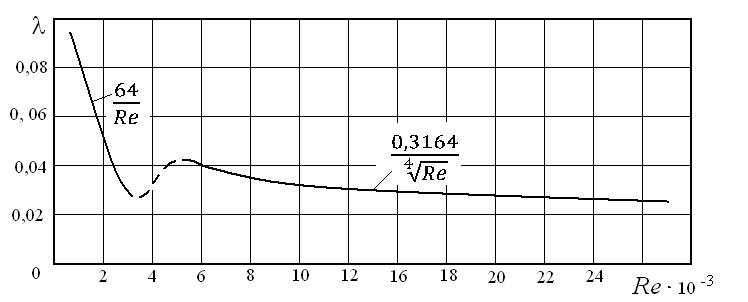
Рис. 5.7. Зависимость коэффициента трения от числа
Рейнольдса при ламинарном и турбулентном режимах течения
в гидравлически гладких трубах
