Теория деформации, основанная на физических закономерностях о сжимаемости и деформируемости сред

В качестве прообраза используемой общей модели неидеально упругой среды Гуревич Г.И. /22/ предложил поликристаллическое тело, состоящее из "частиц" и "прослоек", находящееся при таких температурах и условиях нагружения, когда его необратимая деформация происходит преимущественно за счет смещения кристаллических зерен относительно друг друга. Эти зерна являются частицами модели, а среда в области контакта представляет собой материал "прослоек". Необратимая деформация поликристалла может быть результатом деформирования плоскостей раздела внутри зерен и соответствующих скольжений одних частей кристаллической решетки относительно соседних в направлении выравнивания напряжений в каждой точке макроскопически сплошного тела. Роль прослоек играют дислокации, находящиеся внутри зерен в областях контакта плоскостей скольжения; микрочастицы - части решетки, смещающиеся по плоскостям относительно друг друга. Необратимая деформация поликристалла может быть одновременно результатом внутризерновых перегруппировок атомов, обуславливающих сдвижение частей зерен относительно друг друга и межзерновых перемещений, приводящих к сдвижениям зерен в целом. Для полноты обозрения рассматриваются различные состав и строение самих зерен материала, которые характеризуются различной энергией вырывания молекул и атомов.

Использование теории /22/ долгое время оставалось затруднительным из-за большого числа трудно определимых физических констант, которые входили в уравнение движения, получаемые на основе физических предпосылок. В работе Левшина А.Л., Ратниковой Л.И. и Сакс М.В. /23/ выведены простые расчетные формулы для тела Гуревича /22/, позволяющие прогнозировать скорости и поглощение как функции частоты.

Согласно /21, 23/, при малых касательных напряжениях полная сдвиговая деформация, например, 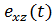есть сумма упругой и упруго релаксационной деформаций: 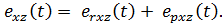Причём 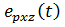обладает непрерывным спектром времен релаксации 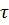с ядром 1/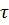

.

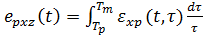В реальных средах соотношение для верхней и нижней границ времени релаксации имеет вид 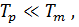а 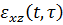подчиняется уравнению состояния типа Кельвина-Фойгта

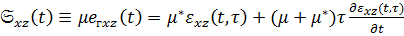. (1.43)

Здесь 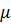- гуковский модуль сдвига, 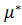- упруго-релаксационный модуль. Аналогичные формулы имеют место для полной дилатации
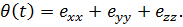В соотношение (1.53) для диллатации вместо 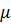и 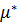входят К и 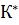- гуковский и релаксационный модули сжатия. Интегрирование (1.53) для скорости полной деформации 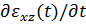и аналогичного уравнения для скорости полной диллатации 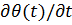приводит к следующему виду для выражений, связывающих деформации и напряжения.

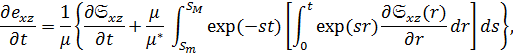
	(1.44)

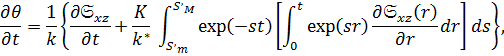
где

,

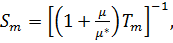
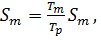
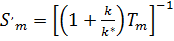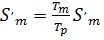
Рассмотрим как в работе /24/ получены выражения для дисперсии декремента затухания и фазовой скорости на примере поперечных волн. Если продолжить спектр времен релаксации в (1.44) до 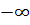, учитывая при этом, что 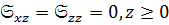и подставить уравнение движения

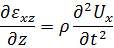
в (1.44), то получается одномерное волновое уравнение в перемещениях

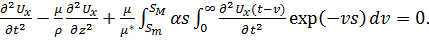(1.45)

Решение ищется в вид

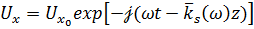, (1.46)

тогда для (1.45) имеем

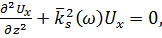(1.47)

где

,

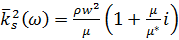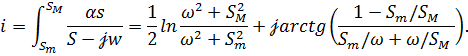
Поскольку фазовая скорость 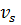и декремент затухания 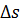плоской гармонической волны связаны с комплексным волновым числом соотношением

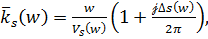(1.48)

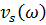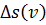то используя (1.47) можно получить зависимости и . Аналогично можно получить выражения для 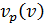и 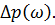Для упрощения получающихся сложных выражений приняты следующие допущения:

· диапазон времен релаксации достаточно широк: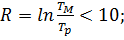

· гуковский и упруго-релаксационный коэффициенты Пуассона поло-жительны и удовлетворяют соотношениям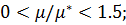

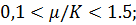
· релаксационные соотношения при объемном сжатии выражены в горных породах слабее, чем при сдвиге: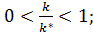

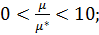
· используется упрощение:

;

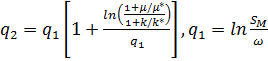· частотный диапазон ограничен следующим образом: для пород с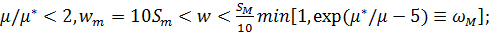

для очень "мягких" пород 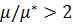диапазон более узкий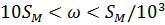

Точность такого приближения – 97%. Исходя из приведенных выше

допущений получены зависимости скоростей и декрементов поглощения,

если известны их значения на опорной частоте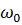

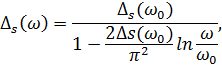
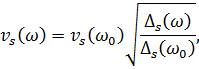
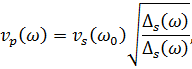
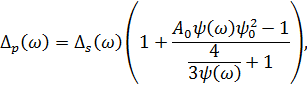
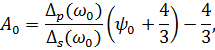
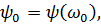
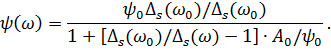
(1.49)

До сих пор мы рассматривали волны, получающиеся в результате решение одномерного волнового уравнения. Рассмотрим обобщенные волны имеющие место, когда в среде присутствуют обменные волновые эффекты. Если сейсмическая волна распространяется в плоскости ХOZ декартовой системы координат под углом r к оси OZ, волновое число в случае решения двумерной задачи, представляется в ви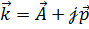де , где 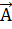– направление максимального затухания, 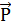- направление распространения волны. В этом случае решение представляется в виде

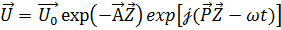, (1.50)

где 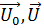- начальная и текущая амплитуды колебаний. При подстановке (1.50) в двумерное волновое уравнение типа (1.47) для комплексного волнового числа 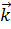получаем

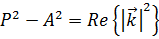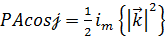, . (1.51)

Таким образом в случае отдельного распространения продольных и поперечных колебаний имеем дисперсионные зависимости для скоростей и декрементов затухания в виде (1.49). А в случае двумерной неидеально-упругой среды комплексные волновые числа представляются соотношениями (1.51).