2015-06-04
185
Пусть в некотором объеме V тела, ограниченного поверхностью S, распространяется сейсмическая волна. Согласно первому началу термодинамики для отрезка времени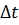 
имеет место соотношение: выполненная механическая работа + количество выделенного тепла = увеличению внутренней и кинетической энергии тела. Второе слагаемое левой части равенства можно представить в ви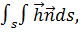де 
где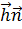 
- скорость распространения тепла через единичную площадку, перпендикулярную единичному вектору 
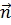. Адиабатическая деформация - характерное явление в сейсмологии для длин волн больших нескольких миллиметров /17/, поэтому 
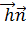, = 0 и, следовательно, энергия механических колебаний должна переходить во внутреннюю и кинетическую энергию частиц среды.
Обширные данные о затухании сейсмических волн приводятся в работах /17-19/. Для получения этих данных авторы используют результаты полевых и лабораторных исследований горных пород /16/. Большое количество данных о диссипации энергии сейсмических волн привело к необходимости построить теорию, которая давала бы возможность одновременно учитывать затухание распространяющихся Р и S волн, а также определять значения волновых диссипативных параметров в области сейсмических частот.
Классическими моделями, описывающими неупругое поведение сред являются: тела Кельвина-Фойгта, Максвелла и стандартное линейное тело /12/. Отметим отрицательные явления, характерные для классических моделей, а потом запишем уравнение с последействием, где они отсутствуют. В теле Кельвина-Фойгта при уменьшении релаксационных модулей до нуля, т.е. при переходе к гуковскому телу, имеем уменьшение продольного и сдвигового напряжений, что противоречит молекулярной сущности деформации. В теле Максвелла при фиксированном напряжении деформация неограниченно растет, поэтому уравнение имеет смысл только для сдвиговых напряжений, когда тело течет. В стандартном линейном теле отсутствуют отрицательные свойства отмеченные для тел Кельвина-Фойгта и Максвелла. Однако, горные породы ведут себя при распространении волн существенно иначе, чем это можно предвидеть при помощи классических моделей. Это объясняется одновременным существованием множества диссипативных механизмов. Кроме того, из уравнений движений, в которых используются все три типа тел, следует существенная зависимость декрементов затухания от частоты, что противоречит большинству опытных данных.
Еще в 1876 году Больцман /17/предложил следующий вид уравнения состояния:
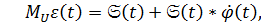(1.39)
где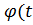 
) - функция крипа /17/, последействия, функция памяти, 
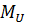- релаксационный неупрзпгий модуль, 
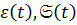- деформация и напряжение для одномерного случая. Многие исследователи занимались подбором 
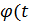) для получения согласия с экспериментом зависимостей фазовой скорости и добротности от частоты /18,19/. Основоположной здесь следует считать работу Николаева Б.Г. /18/, где показано как соответствующим выбором ядер последействия для уравнения (1.39) можно переходить к тем или иным моделям неидеально упругих сред (Больцмана, Дерягина) и определять диссипативные характеристики с использованием метода итераций.
Рассмотрим кратко другой эмпирический подход, основанный на дисперсионных соотношениях зависимости между скоростью и коэффициентом затухания гармонических колебаний (соотношениях Крамерса-Кронига). Используя известную эмпирическую формулу коэффициента затухания /17/
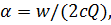(1.40)
где СQ - угловая частота. c - скорость волны, Q - постоянная добротность; импульс распространяющейся волны можно представить в виде
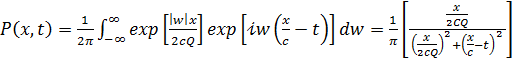(1.41)
Форма этого импульса не совпадает с опытом в следующем /20/:
· (1.41) описывает кривую симметричную относительно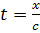 
, реальный же импульс имеет время затухания намного больше, чем время возрастания;
· экспериментальный импульс имеет наклон возрастания приблизительно в полтора раза меньший чем в (1.41). Для обхода указанной трудности Футтерманом /21/ предложено ввести дисперсию скорости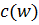 
. Далее в работе /21/, исходя из того, что давление распространяющейся волны отсутствует там, куда не пришло возмущение от источника
, 
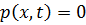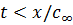; (1.42).
где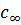 
- максимальная скорость распространения гармонической волны; получены дисперсионные соотношения между скоростью и коэффициентом затухания гармонических колебаний.
Из экспериментальных данных известно, что Q чаще всего постоянно в области сейсмических частот /20/, поэтому в (1.40) подбирается такой закон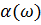 
, не обязательно линейный, для которого Q эффективно постоянно в области исследуемых частот. Далее по известной функции α(ω), определяется дисперсия фазовой скорости 
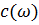из соотношений Крамерса-Кронига.
Таким образом, получаются эмпирические выражения для α(ω), Q(ω) в неидеально-упругой среде. Интересно, однако, получить дисперсионные соотношения исходя из физических законов о деформируемости сред. Соответствующая теория изложена в следующем подразделе, она разработана Гуревичем Г.И. /22/.
